If you store the energy chemically, you can store an almost arbitrary amount.
How would it work exactly? Creating hydrogen or somehow making synthetic hydrocarbons? What's the efficiency like?
Though I'd say if you want to use wind energy and have half-decent way to make it produce chemical fuels then that's the only thing you should do with it, not produce electricity. It's far easier to transport those fuels and there is almost no problem with "lag" with them. Making the wind turbines produce fuels and burning them again for electricity is just horribly inefficient.
The U.S. strategic oil stockpile holds 750 million barrels (25 million m^3).
http://www.nationmaster.com/graph/ene_oil_con-energy-oil-consumption
And US uses aroudn 19 million barrels a day so that 750M lasts for around 40 days. For a sense of how big amount it is then 25 million m^3 is a cube of 290m at each side.
Again, I'm not looking for wind power to displace all other sources of enery overnight
That obviously goes for every kind of energy source.
When, not "if", we have the capability to store 24 hours worth of consumption we can expand wind power production to 50% of total usage in an economically viable way.
24h is way too little if you still want to use it for electricity. Half a week is almost enough when half of all energy is produced by wind.
But I cringe at the title of "denier". "Skeptic" is acceptable, but I would prefer "alternative scientific view". Like, Evolution versus Intelligent Design.
You do realize that ID is not a scientific view by any measure, right? Though I guess then it does make a pretty good analogy for your views on AGW

there are solutions to the storage problem. the "best" one is hydro. it cost 1.4 times the energy to pump the water up there but it can go from 0 production to a couple hundred megawatts is 15minutes.
Yeah but that kind of pumping requires so humongous investment in building dams that it's just mind boggling. Linking again to my favourite analysis on the subject:
http://physics.ucsd.edu/do-the-math/2011/11/pump-up-the-storage/
There he assumes 2TW of usage for US and one week of storage. Currently US has 78GW of installed hydroelectric power or around 4% of what's needed. Also he assumes around 90% of efficiency at converting the pumped water back to electricity. Rather generous but won't really matter much in the end considering the scale of things.
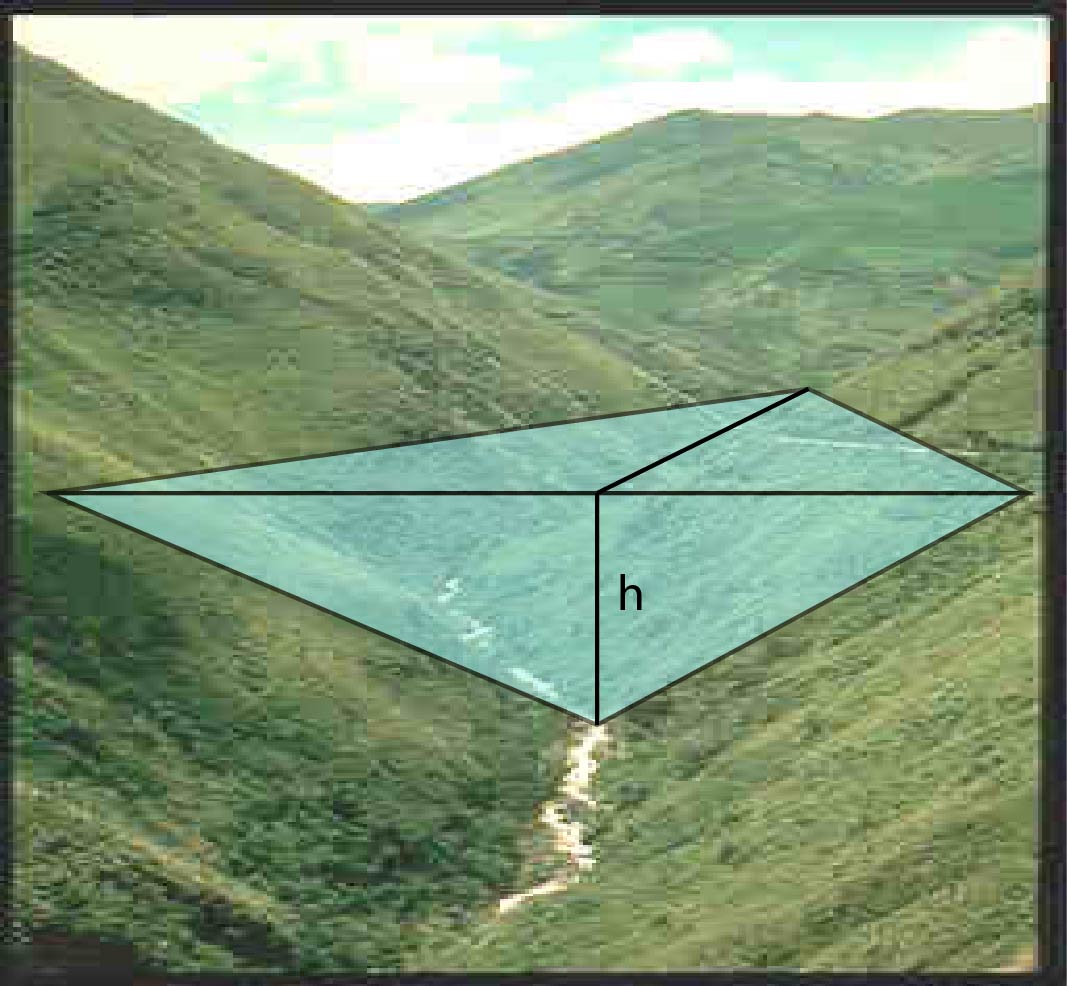
In any case, let’s not allow these details to prevent us from doing some math! Let’s say our average candidate hollow allows a 500 m high wall (1650 ft) on one end, and another few-hundred-meter wall lower down for the lower reservoir (the hollow is wider here—maybe even a vale by now—so the same volume is accommodated by less depth and more area).
Simple model for filling a hollow with water to height, h.
My model for the hollow will have a V-shaped profile, with sides at a 20% slope and the hollow floor running up at a 10% slope. Thus the 500-m-high dam wall is 5 km across at the top, and the lake extends 5 km back in a triangle. This geometry produces a reservoir 2 cubic kilometers in volume. Considering the tapering shape, the stored gravitational potential energy is 2 billion kWh. We just need to build 170 of these things. Never-mind the fact that we have never built a wall of such proportions. Or the fact that the largest pumped storage facility to date stores 0.034 billion kWh—60 times less capacity
.
How it would look like:
But let’s continue to play the game: If we indeed demanded 2 TW of power from about 170 pumped-hydro stations, we’re talking 12 GW of production capability each. This is significantly larger than the biggest hydroelectric installation in the U.S. (Grand Coulee, at 6.8 GW). Times 170.
Dropping the dam height from half a kilometer to "only" 250 meters (Hoover dam is around 200m) would mean we need 16 times more of those or around 2500.
What about building the dams?
These dam walls will require a lot of concrete. A survey of dam construction suggests that the base thickness is approximately 65–90% the height of the dam. Picking 75% and tapering to a cusp, our foregoing geometry requires a concrete volume 25% larger than h³, where h is the dam height. For our 250 m set of dams, we need 19 million cubic meters of concrete apiece. Each dam then contains as much concrete as exists in the Three Gorges and Grand Coulee dams combined! And this is the “small” version of our dams. And we need over 2,500 of them. I’m just sayin’.
At an energy cost of 2.5 GJ per ton of concrete, and a density of 2.4 tons per cubic meter, we end up needing 32 billion kWh of energy per dam, and 90 trillion kWh total. This over 250 times the amount of energy impounded by the dams, and represents three years of the total energy appetite of the U.S. today.
So around 47 billion m^3 of concrete for the dams or a little less than 50km^3, a cube at little more than 3.6km at each side. You can build ~19000 great pyramids with that concrete

And land usage:
In the 500 m dam-height model, the area of the upper reservoir is 12.5 square kilometers. Times 170 reservoirs is 2125 square kilometers. In the 250 m model, we have 3 square kilometers per reservoir, or 8500 km² for the whole set. So the total necessary area scales like the inverse square of the characteristic dam height.
We also need to add the area for the lower reservoir. Since the terrain is likely less sloped lower down, let’s assume that the lower reservoir surface area is twice as big as the upper reservoir, so now we have about 25,000 km² in new lake area (both reservoirs are not full at once, but this land is no place to build a mall).
So yeah, energy storage is MASSIVE problem with any kind of renewable energy. Even if we drop the wind production to "only" 50% and require "only" 24h of storage we still can only make the numbers ~14x smaller. Doesn't help really, still pretty much as unfeasible as before.
For other storage methods (flywheels, compressed air, regular batteries, lifting rocks etc) see this:
http://physics.ucsd.edu/do-the-math/2011/09/got-storage-how-hard-can-it-be/. Hint: they are far worse than pumped water in terms of efficiency.