G80 programmable power
- Thread starter Pigman BABY!!!
- Start date
Anarchist4000
Veteran
Efficiency really depends on what kind of data you're doing. Vec3+1 won't necessarily perform poorly at processing scalars if you have a 1:1 ratio of Vec3 to scalars and they aren't dependent on eachother. And I think it can safely be said that most of the numbers involved in graphics and 3D physics are Vec3's. Heck something like Vec3+1+1 might also work equally well, sort of a mix of both worlds.
Also what would the transistor/die size difference be between a Vec3 MADD and scalar processor capable of performing every instruction? I'm sure the special functions take up a fair amount of transistors.
Also what would the transistor/die size difference be between a Vec3 MADD and scalar processor capable of performing every instruction? I'm sure the special functions take up a fair amount of transistors.
Jawed
Legend
Ha! yeah, I can't crunch it up like that because of the dependency chain (I thought I was in the clear as long as there was one-clock difference, but I was forgetting the entire width of the MAD unit needs to have its source operands ready).
In fact I can't see any opportunity to crunch this up. So, which holes are superfluous?
Jawed
Jawed
Legend
In a unified GPU there's perhaps some conflict between the most common parallelism for vertex shaders versus pixel shaders. In older GPUs, VS pipelines seem to be based upon vec4+scalar, while PS pipelines are based upon vec3+scalar (or vec4).
This thread introduced the concept of the Multifunction Interpolator (which also performs SF):
http://www.beyond3d.com/forum/showthread.php?t=31854
if you do a search on Multifunction Interpolator you'll get a decent selection of stuff (from other threads, too) to read on how NVidia designed for compactness in the SF units. At the same time, transistor efficiency was improved by implementing interpolation functionality there, too - principally by extending the look-up tables to cover both types of calculation (as there's a large overlap between interpolation and SF) and partitioning the calculation into parallel pipeline stages.
There are ATI patent applications on a similar subject:
Method and system for approximating sine and cosine functions
which appears generalisable to more than just SIN/COS.
In my view the FLOP utilisation losses that a conventional vector ALU suffers when one or more components idle are just too much of a red rag to a bull for the IHVs. NVidia has already tackled it, arguably once and for all. It's my suspicion that R600 is also built to maximise FLOP utilisation, but I think by way of packing pixels to fill empty components (e.g. doubling the pixels issued per clock when a vec2 instruction is issued).
In the SM2 days, I suspect, utilisation loss didn't matter an awful lot because shaders were usually dominated by TEX operations. You might also argue that the complexity of implementation of G80's scalar or R600's packing was complete overkill for that era, too.
Jawed
Anarchist4000
Veteran
I'd agree they have to be doing some sort of packing. With no hints that the ALUs are running at 2x the core clock for ATI it's highly unlikely they're going scalar. Which brings on the question which setup is easier to pack for? While Nvidia did make the SF more compact it's still not as small as a MADD and other than GPGPU work it just doesn't seem like the SF would show up very much.
Things might get a bit interesting but what about 4x the pixels instead of 2x. That should make packing substantially easier. Vec1->Vec4, Vec2->2*Vec4, Vec3->3*Vec4. Something like a Vec4+SF would be very similar to xenos but with improved packing to increase efficiency. Vec3/4 could still benefit from the cross/dot operations and anything smaller could be pushed through sideways to keep the hardware happy. If anything branches just kick it back out until you find more of em. Besides the memory bus is 512bits. It'd make sense if they were passing around 512bit data units.
I think ATI mentioned somewhere that R600 was to be Xenos done right or something to that degree. Other than the SF they should be able to keep most of the ALUs working happily regardless of the type of data going through. The SF I suppose could even be part of a TMU if those are becoming programmable.
Things might get a bit interesting but what about 4x the pixels instead of 2x. That should make packing substantially easier. Vec1->Vec4, Vec2->2*Vec4, Vec3->3*Vec4. Something like a Vec4+SF would be very similar to xenos but with improved packing to increase efficiency. Vec3/4 could still benefit from the cross/dot operations and anything smaller could be pushed through sideways to keep the hardware happy. If anything branches just kick it back out until you find more of em. Besides the memory bus is 512bits. It'd make sense if they were passing around 512bit data units.
I think ATI mentioned somewhere that R600 was to be Xenos done right or something to that degree. Other than the SF they should be able to keep most of the ALUs working happily regardless of the type of data going through. The SF I suppose could even be part of a TMU if those are becoming programmable.
Jawed
Legend
The Hexus report of 2GHz being the target is a hint - though many round here treat it with total derision. I interpret that as a hint that the ALU pipes are targetted to run at 2GHz with the rest of the GPU running at 1GHz.
Separately there are so many patent application documents that refer to just 2 operands being fetched, it seems like a strong hint that R600 is 2-clock MAD. If that's the case, then I don't think it's a huge leap to the ALUs being simplified but fast, i.e. 2GHz (or 2x main clock, whatever that ends up being).
Special functions seem to be used a reasonable amount.
The MI/SF unit in G80 is a bit peculiar because for each clock it can produce either a single SF or it can produce four interpolated values - so it's a bit deceptive. It's quite clever because the four interpolation calculations all share a single look-up table (well, set of tables). So, most of the effort goes into interpolation.
I don't understand. If the array is 32 components wide, then it can either process 8 vec4s, 16 vec2s or 32 scalars in parallel (the odd one out being vec3, prolly 8 of those in parallel).
The problem with packing seems to me to be primarily one of fetching the operands. I posted some thoughts on a staggered striped register file in the R600 thread.
There's a few video processing related patent applications that explicitly describe some intriguing data-routings from operands to multiple ALU components (in parallel) that are almost enough to support my packing theory...
Yeah I'm thinking that once you can do packing, it also dramatically improves dynamic branching.
From the patent I linked earlier:
I think this is a strong hint that R600 uses an 8-clock macro to perform SF calculations. And I like to infer that every ALU in the SIMD array can perform the SF calculation in parallel. Though the patent describes significantly lowered precision being adequate for some of the multiplies which mitigates against that theory.
Jawed
Anarchist4000
Veteran
I didn't necessarily mean that the array is 32 components wide. Just a multiple of 4 to improve the packing. Each operation should be working on a full packed Vec4 with the exception of dot/cross products on a Vec3. Ideally the benefit of processing a vector instead of scalar would cover the hit of one component not doing anything for a vec3 cross/dot product. Any non vector based operations(add,sub,mul,div) would get processed vertically, the vector based operations(dot,cross) would go through horizontally. Just grab the corresponding components from each of 4 pixels being processed.
x+y=[xxxx+yyyy]
xyz+zxy=[xxxx+zzzz][yyyy+xxxx][zzzz+yyyy]
xyzw dot xyzw = [xyzw dot xyzw]
Now using a 4 wide ALU you'd bring in up to 512bits of data, select all the like components, then keep running them through until you've hit every component. Hope i'm not to off topic, didn't realize this was the G80 thread until now. But this does seem like an ideal way to pack a vector.
Last edited by a moderator:
Jawed
Legend
Ah, OK, I suspect we're in agreement, but because I didn't venture into DP territory with that example code, I haven't worked it through. DP is obviously a win in G80.
I should rework the pipeline pizzas based on some code with a DP3 in it, say... Hmm, I could put one in at the end instead of the final MUL...
Jawed
Jawed
Legend
I've revised the code example to include a DP3:
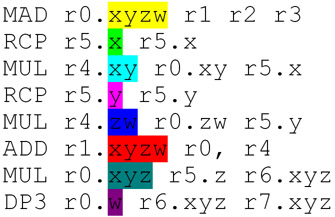
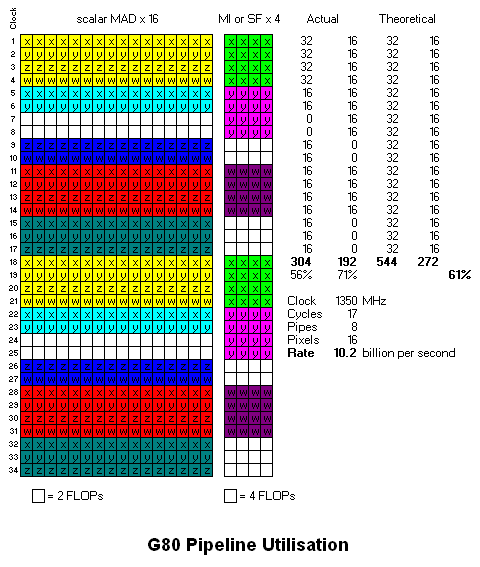
so this is how I think it executes on G80:
Bob, sorry, I realised a problem with the prior code example: I made a boo-boo in the MUL r4.zw line, multiplying two scalars, unintentionally
meaning that the MAD's z and w components could have been calculated later - which is, I think, what you were alluding to when you said "MAD limited".
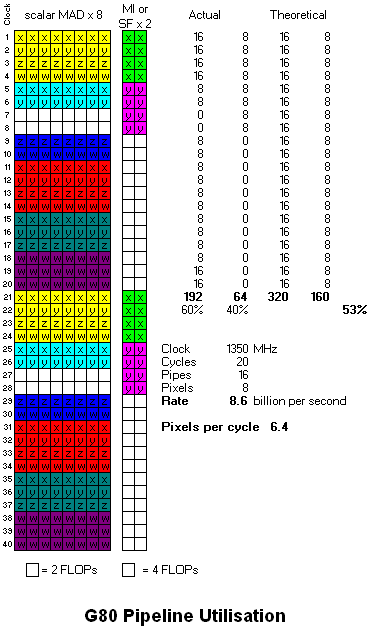
Here is how I think the code would execute in R600:
where I have revised the MUL r0.xyz to issue as three successive scalars as Bob suggested. The DP3 takes two cycles longer than G80 because each component operation (MUL or ADD) stands alone, there's no MAD. Also I have made SF take 8 clocks, as inferred from the patent.
I've added "Pixels per cycle", showing that G80 and R600 have the same rate here, 6.4.
Jawed
so this is how I think it executes on G80:
Bob, sorry, I realised a problem with the prior code example: I made a boo-boo in the MUL r4.zw line, multiplying two scalars, unintentionally
meaning that the MAD's z and w components could have been calculated later - which is, I think, what you were alluding to when you said "MAD limited".Here is how I think the code would execute in R600:
where I have revised the MUL r0.xyz to issue as three successive scalars as Bob suggested. The DP3 takes two cycles longer than G80 because each component operation (MUL or ADD) stands alone, there's no MAD. Also I have made SF take 8 clocks, as inferred from the patent.
I've added "Pixels per cycle", showing that G80 and R600 have the same rate here, 6.4.
Jawed
Jawed
Legend
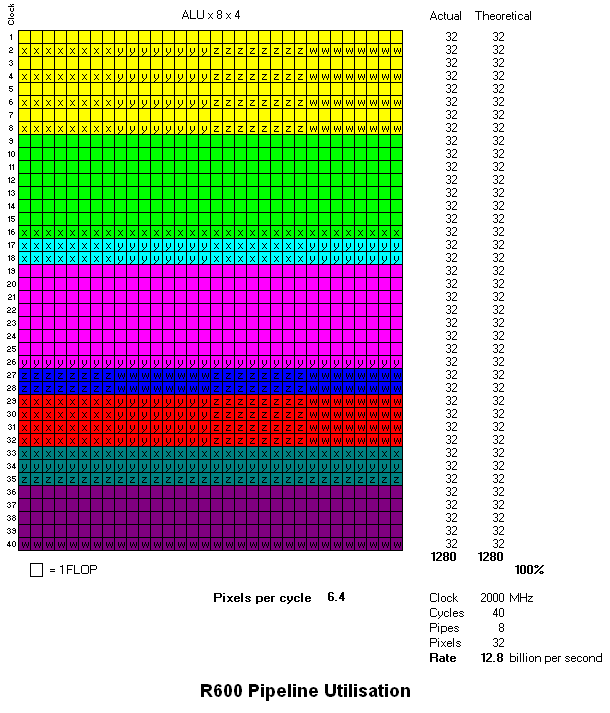
For completeness, I've included the other GPUs:
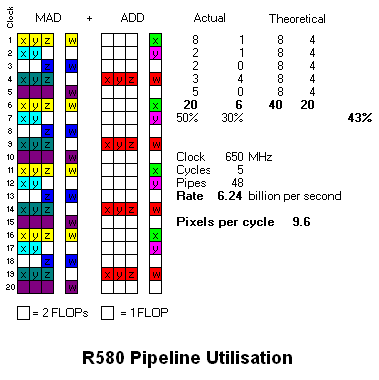
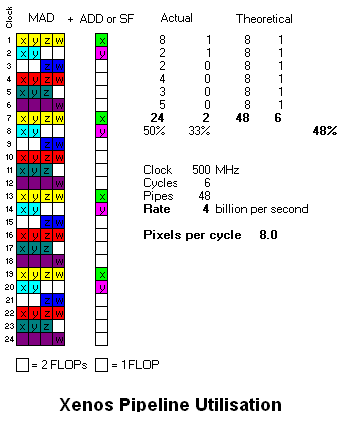
I suppose for the time being the best comparison of scalar and vector architectures is between G80 and Xenos.
G80 trades a lower throughput per cycle against the fact it's designed to clock far higher. If Xenos were 600MHz and 64 ALU pipes it would have the same rates for this particular piece of code, but it would be doing so at lower FLOP efficiency, 48% versus G80's 53% - implying, perhaps, that G80 consumes ~10% less die area for the same throughput. But that's prolly a leap too far
Jawed
Last edited by a moderator:
Jawed
Legend
Well, that would cost me about $1000 since I'd need an entirely new PC: mobo, CPU, memory, power supply; as well as G80.
Actually, I was wondering if I could test this stuff using:
http://developer.nvidia.com/object/nvshaderperf_home.html
but it doesn't look like
Jawed
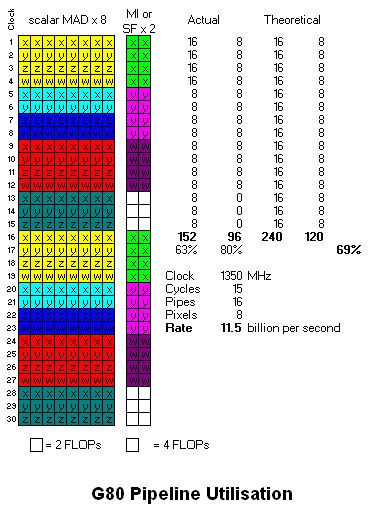
Jawed: the G80 scheduler afaik sees three kinds of units: ALU, TMU, SFU. The SFU is not part of the ALU pipeline, so all that matters is the average ratio (as long as the pipeline is filled, that is!)
As such, the G80 would get 100% utilization in your test shader. This is what Bob means when he said that you shouldn't have holes in your MADD pipeline.
Uttar
As such, the G80 would get 100% utilization in your test shader. This is what Bob means when he said that you shouldn't have holes in your MADD pipeline.
Uttar
Jawed
Legend
Bob said I was violating instruction dependency, and you're saying the instruction dependency can be avoided by multi-threading.
These statements seem to be in direct contradiction
Jawed
They would be, if they were referring to the same diagrams! Bob's comment was on an earlier one.These statements seem to be in direct contradiction
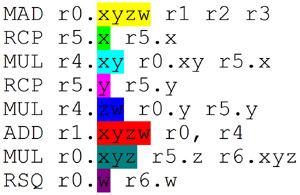
In this diagram, the blue instruction begins before the purple one finishes, even though they are dependent.
And then, Bob's comment on being ALU-limited was regarding this:
Where other threads running the same program (or even another one!) will fill in the MAD holes! As such, your diagram scheme cannot represent the G80's pipeline correctly, since the SFU is not part of the ALU pipeline per-se, but rather seen as a distinct unit by the scheduler. It also cannot represent TEX instructions on any architecture but the G7x, since they are also seen as a distinct unit to the scheduler for R5xx/Xenos. And I'm also fairly sure every SFU op you got in there is going to take an ALU cycle for G80, since the ALU pipeline is used to setup the value to be "in range" for the SFU.
Uttar
Similar threads
