Just had a look at their FAA... it seems to be some kind of edge only, coverage mask technique. I am a bit confused by their mention of "fragment buffer". I wonder how big this fragement buffer is and what it contains. Things are easy if you assume one possible fragement always covering a full pixel behind it (you would just need to store 2 colors and a coverage value) however if you have multiple fragment cases for the same pixel it gets complicated, but I guess you could ignore those.
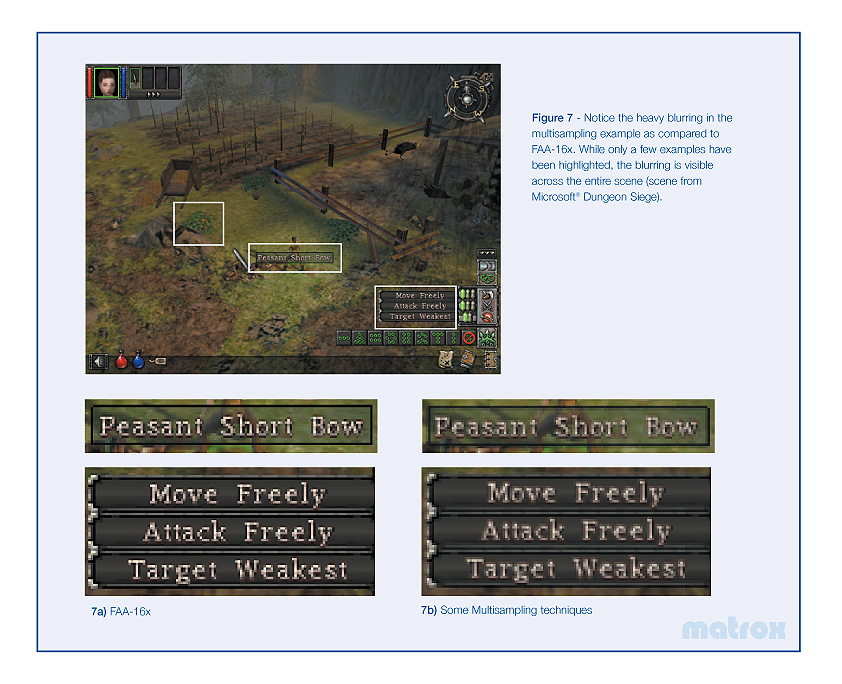
The picture with the dragon and their stats numbers are misleading, they show an edge detect image and numbers but reality is that they do this "per triangle edge" as indicated in the text and you have way more triangle edges than indicated in their dragon image. They make it sound like they only do extra work and processing on 3.2% of the pixels, that number is probably much higher in reality assuming they do this per triangle edge (both visible and hidden). Sounds like a marketing twist.
I also wonder if they need a post processing phase where they process the fragment buffer and frame buffer into the final result.
I also wonder what happens to triangle intersection edges. Say I have a black and white triangle intersecting (Z test) this would give an aliased edge, if they only process the triangle "edges" this "intersection edge" might not be AA unless they detect and flag these intersection edges as well.
I suspect they have the frame buffer and the fragment buffer. The frame buffer contains full pixels, the fragment buffer contains the color of the fragment and a coverage value (ranging from 1 to 15, if its 0 it means there is no fragment on top fo the full pixel already in the framebuffer). So if a pixel is a triangle edge pixel you write the color of that triangle edge pixel into the fragment buffer and include a coverage value, the framebuffer contains the old background color (can be the clear color or the color of a previous polygon). The Z value is updated with the edge Z value. If another polygon overwrites this edge you would need to overwrite the framebuffer and the edge info should be invalidated somehow (this seems to indicate that extra BW is still required but not as much as with other techniques - MS of FSAA uses say 4 samples so you write 4 colors to the buffers, this system only writes 2 colors and a small coverage value, so less BW is used). Tricky bit is if you have an edge and its covered by another edge, I guess in that case you can force an update of the framebuffer with the old edge info and then add the new edge info into the fragement buffer. Hmm... wait... what if I insert a different colored polygon at a later time behind an already written polygon, this might update the background color. Original info might be from a clear (black) with an edge (white poly ) but I then insert a blue polygon in front of the clear but behind the white triangle... I would want a blend between blue (tri) and white (tri) and not between black (clear) and white (tri), how do you know you need to update the framebuffer (background) color. Hmm guess you need 2 Z-values as well, one for the background fragment and one for the edge fragment.
Definitely seems to have a BW advantge over other techniques :
MSAA = upsampled frame buffer and Z buffer = upsampled with the number of samples = for example 4 samples means 4 times the color and 4 times the depth buffer needs to be stored = say 32 bit Z and color = 32*4+32*4= 256 bits per pixel
Matrox FAA = only 2 buffers, background fragment buffer and edge fragment buffer, both need color and Z info and a special coverage value. = 2*(32+32)+4 bits (coverage mask value) = 132 bits per pixel
Nice saving at first look... also the FSAA MSAA techniques also require a normal size buffer (so you need one set of upsampled buffers and then multiple normal resolutions buffers that you combine into), this technique only needs a normal resolution buffers set (dual or tripple buffering) and a fragment buffer. You process the fragment buffer into the background fragement buffer in a post process phase.
Note its late so possibly I am missing some bits and bops about this technique, might even be wrong