The Nature of Scaling (Signal Processing Edition)

[Albuquerque]

Albuquerquue, I don't think you've understood what Xmas has been saying.

No, I get it exactly, but I must not have been clear in the way I described it. Shifty seems to have the same idea I do, because he re-explained what I was trying to say here:

The intrinsic nature of the upscale from singularity sample to area of light of an LCD doesn't have any obvious bearing on the conversion from an area of samples to a larger array of samples. The LCD upscale is out of our hands. We can only work with the array of samples that will be transmitted to the display device.

We can only work with the display technology that we have. Thus, arguing pixel size is a semantics argument at best. Pixel sizes are what they are, but that's not what we 're talking about.

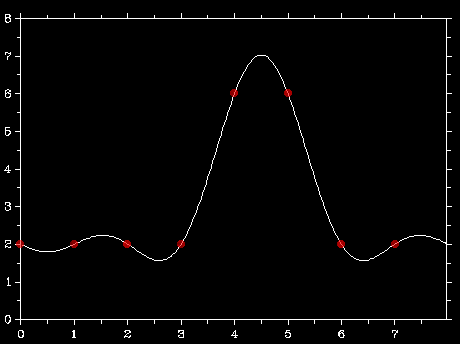
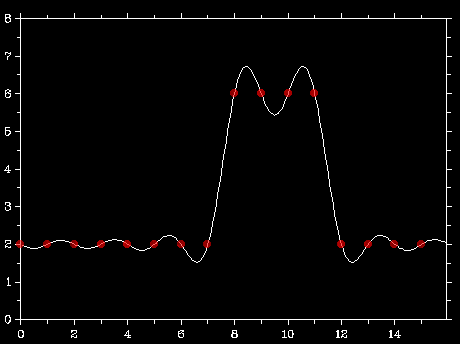
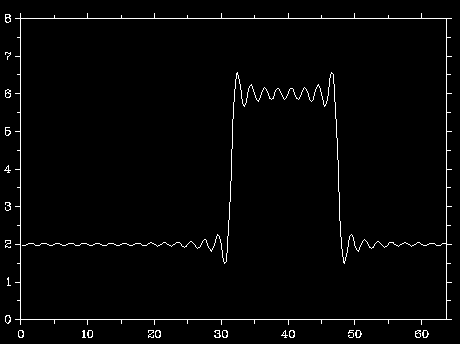
We're talking about non-native-res frame being resampled. I'm pretty sure that's been the discussion point that Xalion has been mentioning this entire time, even though a few people have now attempted to derail it into something else.

Rescaling of the digital image is the discussion. Not the pixels. So again, show me a method of rescaling an image that doesn't do exactly what Xalion has described, and I'll finally understand what we're trying to get at. But for now, all I see is red herrings...

 

[Albuquerque]

Ok, I thought of a much better way to describe why pixel size is irrelevant to this conversation:

Your 50" 1080P TV is not going to "grow" bigger pixels to upscale your content. Nor is it going to "grow" extra pixels to upscale your content. Your TV is a fixed-resolution device, the 2,073,600 discrete picture elements are set layers of glass and silicon and are not going anywhere.

Thus, you have two options: display at native resolution (meaning your less-than-1080P signal is going to display at a size that does not consume the entire 50" of display area), or else display via upscaling that we've been trying to address in this discussion since post 1.

If we really can't agree on this, then I want to know where I can purchase a display device that will allow me to grow these HUGE pixels, or grow extra pixels for proper scaling. Otherwise, all this pixel talk is still a red herring.

 

[Xmas]

Here is an image of a reconstructed signal for the sample sequence [ 2, 2, 2, 2, 6, 6, 2, 2 ]. The sample points are also marked red.

Here is a reconstructed signal for the "pixel doubled" sequence, i.e. [ 2, 2, 2, 2, 2, 2, 2, 2, 6, 6, 6, 6, 2, 2, 2, 2 ]

And here a reconstructed signal for the 8x upscaled sequence (nearest neighbour sampling):

Am I the only one who would say that the upscaling in this case creates "harder" edges, since it adds higher frequencies?

 

[Xalion]

Actually - those pictures don't look like high frequencies are being amplified.

Instead, it looks like the amplitudes for high frequencies are being depressed as you increase the frequency range. There are a wider range of high frequencies, but with smaller amplitudes. You should post the amplitudes for the actual frequencies.

Also, make sure you specify exactly how you calculated them.

Sorry for the edit - but forgot something. It would help if you normalized the amplitudes so we can actually compare them.

 

[betan]

Sure a very large gaussian footprint can remove most aliasing (not all, because you can not guarantee constructive interference won't raise the aliasing above the quantization threshold) but generally we prefer a little aliasing in our images rather than a lot of blur (and we prefer either to the ringing mess which would result from true sinc footprints).

I don't know who prefers little aliasing (besides the people who actually needs to resolve the pixels) but any bounded convolution matrix (FIR) or reconstruction footprint is an imperfect filter so you are right.

However, the main reason people use Gaussian is that it's as bandlimited in F domain as it is in time (or space) domain, so if you can effort "bigger" matrix or footprint there is not much point using Gaussian anymore.

Imaging is inherently aliased every which way and we like it that way ...

imperfect filters are almost god given, it's not specific to general imaging, yet that "framework of sampling theory" looks to be working well.
I think the fact that people are doing antialiasing, or trying to go beyond 0th order hold for reconstruction/supersampling shows that too.

Am I the only one who would say that the upscaling in this case creates "harder" edges, since it adds higher frequencies?

Upscaling in practice always adds high frequencies, though those may be less than reconstruction noise on your display.
It's trivial to "see" for 0th order or nearest neighbour, since same "changes" occur in much smaller distance meaning high frequency noise. At the same time, it wouldn't be visible on a 1-to-1 mapped display with perfect squares representing pixels.

But why are you doing continues interpolation? Is this supposed to be your TV?
Sorry for jumping in, I haven't really been following that discussion (or any other).

 

[Xmas]

Actually - those pictures don't look like high frequencies are being amplified.

Correct. And I did not claim they were. I said that higher frequencies were added which makes the edges harder.

Upscaling in practice always adds high frequencies, though those may be less than reconstruction noise on your display.
It's trivial to "see" for 0th order or nearest neighbour, since same "changes" occur in much smaller distance meaning high frequency noise. At the same time, it wouldn't be visible on a 1-to-1 mapped display with perfect squares representing pixels.

Indeed, and that's something I wrote earlier in this thread.

On the other hand, if you had two monitors of the same size which showed pixels as perfect flat-colored squares, one with double the resolution in both dimensions, then simple pixel doubling would make the higher resolution monitor show exactly the same image as the other one.

In practice you'll get quantisation noise, but otherwise you could upscale without touching the frequency content.

But why are you doing continues interpolation? Is this supposed to be your TV?
Sorry for jumping in, I haven't really been following that discussion (or any other).

No, it's not meant to show the reconstruction of a specific display device at all.

 

[MfA]

I don't know who prefers little aliasing (besides the people who actually needs to resolve the pixels).

Blur, ringing or aliasing ... pick one. Even if you could practically realize it an imaging system with a brickwall pre-filter (Sinc) at the Nyquist limit reconstructed with the appropriate reconstruction filter (Sinc) would look like crap, ringing all over the place.

However, the main reason people use Gaussian is that it's as bandlimited in F domain as it is in time (or space) domain, so if you can effort "bigger" matrix or footprint there is not much point using Gaussian anymore.

The main reason people use it because it looks okay.

imperfect filters are almost god given, it's not specific to general imaging, yet that "framework of sampling theory" looks to be working well.

It's working well enough ... it's just not all that relevant. Without perfect reconstruction there are no optimal algorithms, only ill posed problems and matters of taste ... with perfect reconstruction there are only fugly images.

 

[betan]

Blur, ringing or aliasing ... pick one. Even if you could practically realize it an imaging system with a brickwall pre-filter (Sinc) at the Nyquist limit reconstructed with the appropriate reconstruction filter (Sinc) would look like crap, ringing all over the place.

That's for reconstruction only, and I would agree a little noise above Nyquist is desirable there.
However perfect sync filter for pre sampling low pass stage is always welcome, though luxurious.
Ripple effect of low pass filtering on constant surfaces won't be "visible" on samples.

The main reason people use it because it looks okay.

It looks okay when you are resource limited and there is a reason for that.
If you are not however, you can do better than a low emphasis filter, I would imagine.

It's working well enough ... it's just not all that relevant. Without perfect reconstruction there are no optimal algorithms, only ill posed problems and matters of taste ... with perfect reconstruction there are only fugly images.

Okay, I guess that was your main point from the beginning.
I agree with that too, especially in the context of upscaling.

 

[Albuquerque]

*raises hand*

Xmas, I'm pretty confident the first two are not being represented properly... Let me say this first tho:

If I'm reading right, nearest neighbor is pixel multiplication that's used to fit a smaller image into a bigger space that may or may not have an even magnification factor for X and Y axiis (what's the plural of axis?) If you did a nearest-neighbor sampling at 2x in each direction, you'd have the same output as a flat pixel doubler so far as I can tell. Thus, I don't see how the lines would be harder -- they'd simply be bigger. The contrast between the two edges isn't going to change.

And that's where I come back to your graphs being represented incorrectly...

Remember this?

Your 50" 1080P TV is not going to "grow" bigger pixels to upscale your content. Nor is it going to "grow" extra pixels to upscale your content. Your TV is a fixed-resolution device, the 2,073,600 discrete picture elements are set layers of glass and silicon and are not going anywhere.

Thus, you have two options: display at native resolution (meaning your less-than-1080P signal is going to display at a size that does not consume the entire 50" of display area), or else display via upscaling that we've been trying to address in this discussion since post 1.

The picture elements in your display device are not going to shrink, meaning that while your written scale was entirely correct on all three graphs, you are a bit misleading in showing them all at the same physical size. Here is a much more "visibly accurate" representation of those graphs (in the same order, only left to right, as you posted)

Because the pixels never change shape, and we never add or remove pixels from the display device, then THAT progression is the more accurate one. Again, your written scales were entirely right, you just weren't "scaling" them correctly for our display...

Edit:
I had to scale those with MSPaint, which I believe uses nearest-neighbor sampling as well for minification -- meaning I lost a bunch of your sinusoidal wave when I shrank 'em to fit properly on the horizontal axis. So I "touched up" your waves with a fatter paintbrush before shrinking them, so my resized waves aren't as pretty as they should be -- so please forgive the scaling error

Hopefully my MaDd paintbrush skillz don't detract from the point I am trying to make.

 

[MfA]

Ripple effect of low pass filtering on constant surfaces won't be "visible" on samples.

Up to about 10% overshoot on pixel opposite a hard edge and it doesn't decay all that fast. An example of a step edge from 0.1 to 0.9 after a brickwall low pass with Nyquist limit cut off :

 

[Xalion]

Correct. And I did not claim they were. I said that higher frequencies were added which makes the edges harder.

In practice you'll get quantisation noise, but otherwise you could upscale without touching the frequency content..

Once again, you really need to post the normalized amplitudes so we can compare. I am asking for a couple of reasons. First, you have defined distance as 1/N instead of going from 0 to 1 in the picture to fit your frequencies. As a matter of fact, you've done exactly what I said should be done earlier by using your transform (DST in this case I believe) to define that distance. Second, it seems like you are saying that a greater number of higher frequencies means more hard lines.

Now, on one hand with the definitions you are using, you will always "add higher frequencies" when you upscale. That is because you will have one frequency per sample in your expansion. With the way frequencies are displayed in your graph and the way you have defined distance, those frequencies will always be "higher". That seems to conflict with your claim that you can upscale without touching frequency content.

Also, it seems that every upscaling adds hard lines according to your definitions. For instance, that would mean this picture (which is just your set of points upscaled using fourth order interpolation) has more "hard lines" than your original.

Here is the same picture using circles at each point instead of rectangles - want to make sure we avoid the whole square thing again:

Both look a lot like gradients to me to be honest. I would have a really hard time claiming either has hard lines. For comparison, here are the points plotted the way you have plotted things above:

So I just need you to clarify by posting the frequencies and showing exactly what you mean as hard lines when comparing the two.

 

[Xmas]

The picture elements in your display device are not going to shrink, meaning that while your written scale was entirely correct on all three graphs, you are a bit misleading in showing them all at the same physical size. Here is a much more "visibly accurate" representation of those graphs (in the same order, only left to right, as you posted)

This example was for pure upscaling of the image, independent of any display device. And I believe it's a perfectly valid POV to take that it's not the image growing bigger but the samples becoming denser. I'm not saying your view is wrong, but mine isn't wrong either. What we can say either way is that the edges are becoming harder relative to the content size. And I think that's the important part.

After all I don't know what monitor the person who wants to see the image is going to use, and I don't know at which distance they're going to view it. Maybe you're scaling the image so you can view it at a more convenient distance? Maybe you're comparing one monitor to another with higher resolution at the same size?

And I'm sure you can find many people claiming that they can view just about any resolution fine on their CRT and would never buy an LCD because of the scaling...

 

[Albuquerque]

This example was for pure upscaling of the image, independent of any display device. And I believe it's a perfectly valid POV to take that it's not the image growing bigger but the samples becoming denser.

I don't agree. While we can sit here and talk about how all of this image data is just a figment of a digital imagination, the only way that we as a species see that data is through a display device.

So let's stop the semantics and talk about how we're going to view it. All current display technology that I'm aware of in any sort of consumer-level production is fixed-element technology. Thus, the only thing you're serving here is some facet that nobody will ever see, and we ARE talking about how humans are seeing this data.

 

[Xmas]

Funny how I brought up this very same point before and got the reply that the discussion was about the digital image content, not about the reconstruction that display devices perform...


And I'll repeat what I wrote before:

After all I don't know what monitor the person who wants to see the image is going to use, and I don't know at which distance they're going to view it. Maybe you're scaling the image so you can view it at a more convenient distance? Maybe you're comparing one monitor to another with higher resolution at the same size?

And I'm sure you can find many people claiming that they can view just about any resolution fine on their CRT and would never buy an LCD because of the scaling...

You seem to be considering only one case: comparing the upscaled and 1:1 mapped image shown on the same device and viewed at the same distance. And I don't think that's the only case to consider.

 

[Albuquerque]

You seem to be considering only one case: comparing the upscaled and 1:1 mapped image shown on the same device and viewed at the same distance. And I don't think that's the only case to consider.

Being as those two options are the entire gammut of options for 99% of the consumer public, I think it's pretty relevant. Actually, that's only if your display device even allows 1:1 pixel mapping, which not all do. But since we're talking about how upscaling destroys the hard edges and high-frequency data that was visible in the original unscaled image (visible, as in, someone is seeing it on a display device) then the only comparison I can make is at 1:1 mapping.

In fact, I'm going to repeat what you said to ensure that you know how much I am considering it relevant -- the average consumer is not going to move their couch away from their television set based on the amount of upscaling done by their favorite console game. Nor are they going to buy a different TV for the various source resolution material they will view.

So, whether it's a 19" screen being viewed from across a kingsize bed (15-ish feet?) or a 50" television being viewed from a comfy couch on the other side of the TV room (20 feet?), the viewing distance nor the output device is going to change.

Yet again, we can sit here and make up corner cases where laboratory experiements can do XYZ, but those are corner cases and are not indicative of what Jane and John C. Doe see in their consumer devices. And their scenario is not different from the vast majority of cases out there -- likely to include yours.

Tell me, do you move your couch / TV based on upscaling content? Even better, do you buy a new TV / monitor depending on the source media resolution?

 

[Albuquerque]

Did we finally concede that we dont' buy new display devices and change our viewing distance for upscaling content?

Or was there some other part that I was missing? I'm catching up from being gone for three weeks

 

[Xmas]

People also compare display devices when they make a buying decision, and some may even buy a larger screen to be able to increase their viewing distance. So no, I still don't agree that the difference on a single device is the only important case.

 

[Albuquerque]

People also compare display devices when they make a buying decision, and some may even buy a larger screen to be able to increase their viewing distance. So no, I still don't agree that the difference on a single device is the only important case.

I could see that, but after Jon Doe convinces his lovely wife Jane of his need for a 96" plasma and finally takes home a 32" instead, that display device is incredibly likely to stay A: in the same place and B: the same size for a very long duration.

So I still don't understand why we're talking about the display device physically changing pixel size, or display size, or viewing distance. The incredible majority of the public isn't going to alter those with anything like enough frequency to make a difference. Thus, yet again, the only place where upscaling has any bearing on pixel element size or viewing distance is purely academic corner-cases at best.