Proposed upscaling technique - render vectors to pixels, convert to vectors, upscale and re-raster *spawn

[jlippo]

well raytracing was impossible and other rendering methods like dreams media molecule where, or ue5. Its always impossible until its done. Thats why humans do things.

Even when with your idea of creating perfect 2D? presentation works, you will need to rasterize or raytrace it to show it on screen.

At that point you lose the perfect resolution and need antialiasing and so on.

What is the goal of creating the 2D vector presentation?
What is advantage over using normal 3D objects?

For framerate doubling and such it certainly sounds excessive.

 

[msaki]

Even when with your idea of creating perfect 2D? presentation works, you will need to rasterize or raytrace it to show it on screen.

At that point you lose the perfect resolution and need antialiasing and so on.

What is the goal of creating the 2D vector presentation?
What is advantage over using normal 3D objects?

For framerate doubling and such it certainly sounds excessive.

you could ask the same for alot of graphics techniques, whats the goal for creating raytracing cores whats the goal for ml hardware, whats the goal for vrs??? unending paradox. the point is aliasing will never be solved simply because of raster images even if playstation 20 comes around with 1000 teraflops you would still end up with aliasing unless you used vector images. New fresh revolutionary ideas change video games. we would still be stuck with 2d games if the 3d revolution didnt come, we would still be stuck with traditional raster tricks if raytracing didnt come. I just dont get the obsession with the current rendering pipeline your its like were forced to believe that this is the only way like some sort of religious cult.

 

[JoeJ]

There's always a need for more boundary pushing and creative algorithms (Look at nanite, which is mostly a cool computer sciency-y tree algo) but game programming is mostly focused on the challenges that exist to get to the next level of complexity with the content we need to ship right now.

But that's exactly the problem: Due to schedule, you have no time and resources to invest in long termed research, so you can only do iterative progress over the established methods, which are all brute force.
Only a tiny fraction of companies seemingly thinks differently, does the investment, which then gives us things like Nanite, which is the only example of gfx tech that is not brute force i could currently list.
The result is that other companies are no longer competitive at all, and so the whole industry switches over to UE, causing stagnation in the long run.

But i don't take the excuse of having tight schedules. It was like that all the time, and still, even when the industry was much smaller, there was more creativity some decades ago. People cam up with BSP trees or fine grained LOD solutions back then, and used it in production successfully. It was diverse and interesting.
So i think the true scapegoat is pixel and vertex shaders. They were not very flexible but fast. Brute force methods became faster than complex hidden surface removal or fancy LOD. So the industry converged at a brute force culture.
Then, compute shaders were introduced, but the devs were already stuck in their pixel shader mindset, and never learned to utilize the new power bringing back all the flexibility we've lost before.
Besides some basic light binning, cluster culling, and GPU driven rendering, compute remained underutilized and not much has changed.

It feels like they don't come up with anything new they have not been shown from NV research papers. But the problem is: NV does not want new efficient solutions so games can run on a potato. They want reasons for people to upgrade, and selling bigger premium GPUs, which is the opposite of what we want.

Thus i really think there should be more investment into research from the gaming industry themselves. But probably it's already too late now.

well raytracing was impossible and other rendering methods like dreams media molecule where, or ue5. Its always impossible until its done. Thats why humans do things.

RT was never considered to be impossible. It always was 'the future', and there were path traced real time games a decade before RTX GPUs came out. (see the Brigade engine)
Point splatting as used in Dreams was used long before as well, e.g. for visualization of 3D scanned data sets. There is still active research on that as well.
Fine grained LOD as used in UE5 was always a major goal, and it also was used decades ago (see Messiah game or ROAM terrains). We also saw 'Unlimited Detail' demos, voxel octrees, Automontage, etc.

Those things did not surprisingly appear out of nowhere. The goals were clearly defined, methods to consider and improve were given, promises and visions were there, research was done.

For your idea that's a bit different: Nobody ever tried to convert 3D scenes to something like 2D postscript in real time. It was not done because there is no advantage to expect. No goal, no hope for better performance or quality.

So if you want to see that happening, you have to work on it yourself. You'll see it won't work, but maybe you come up with something else along your way.

 

[msaki]

But that's exactly the problem: Due to schedule, you have no time and resources to invest in long termed research, so you can only do iterative progress over the established methods, which are all brute force.
Only a tiny fraction of companies seemingly thinks differently, does the investment, which then gives us things like Nanite, which is the only example of gfx tech that is not brute force i could currently list.
The result is that other companies are no longer competitive at all, and so the whole industry switches over to UE, causing stagnation in the long run.

But i don't take the excuse of having tight schedules. It was like that all the time, and still, even when the industry was much smaller, there was more creativity some decades ago. People cam up with BSP trees or fine grained LOD solutions back then, and used it in production successfully. It was diverse and interesting.
So i think the true scapegoat is pixel and vertex shaders. They were not very flexible but fast. Brute force methods became faster than complex hidden surface removal or fancy LOD. So the industry converged at a brute force culture.
Then, compute shaders were introduced, but the devs were already stuck in their pixel shader mindset, and never learned to utilize the new power bringing back all the flexibility we've lost before.
Besides some basic light binning, cluster culling, and GPU driven rendering, compute remained underutilized and not much has changed.

It feels like they don't come up with anything new they have not been shown from NV research papers. But the problem is: NV does not want new efficient solutions so games can run on a potato. They want reasons for people to upgrade, and selling bigger premium GPUs, which is the opposite of what we want.

Thus i really think there should be more investment into research from the gaming industry themselves. But probably it's already too late now.


RT was never considered to be impossible. It always was 'the future', and there were path traced real time games a decade before RTX GPUs came out. (see the Brigade engine)
Point splatting as used in Dreams was used long before as well, e.g. for visualization of 3D scanned data sets. There is still active research on that as well.
Fine grained LOD as used in UE5 was always a major goal, and it also was used decades ago (see Messiah game or ROAM terrains). We also saw 'Unlimited Detail' demos, voxel octrees, Automontage, etc.

Those things did not surprisingly appear out of nowhere. The goals were clearly defined, methods to consider and improve were given, promises and visions were there, research was done.

For your idea that's a bit different: Nobody ever tried to convert 3D scenes to something like 2D postscript in real time. It was not done because there is no advantage to expect. No goal, no hope for better performance or quality.

So if you want to see that happening, you have to work on it yourself. You'll see it won't work, but maybe you come up with something else along your way.

rt, point splatting, atomontage, ue5 where all considered impossible on older hardware and yes some of such techniques could be done long ago but not at the acceptable performance a plasytation 2 could do raytracing and so did nintendo 64 doesnt mean a full on game could handle it.

rt, point splatting, atomontage, ue5 where all considered impossible on older hardware and yes some of such techniques could be done long ago but not at the acceptable performance a plasytation 2 could do raytracing and so did nintendo 64 doesnt mean a full on game could handle it.

and to say that its only my idea and that nobody ever tried and it was not done because there is no advantage! is really unscientific. What if someone does it what are you going to say next? impossible is nothing, just because you cant fathom it doesnt mean its impossible or pointless.

 

[jlippo]

and to say that its only my idea and that nobody ever tried and it was not done because there is no advantage! is really unscientific. What if someone does it what are you going to say next? impossible is nothing, just because you cant fathom it doesnt mean its impossible or pointless.

Question still is, what you want to do with it?
What are the advantages you are hoping for?


Ie.
If one would want to create image upscaler which finds edges like MLAA, samples target image and preserves those found vector edges during scaling, it should be doable.

It has problems like losing subpixel movement of those edges, as it fits them to source resolution, but edges can be sharp.

Also rest of the image would use whatever scaler you want, which could make it blurry in comparison.

 

[Shifty Geezer]

were not talking the same thing, im not talking about geometry triangles or edges im talking about the final rendered image on a frame buffer that is stored as a bitmap to be transformed to a vector image instead this will kill aliasing since vectors have infinite resolutions

I don't understand what you mean by 'vector image'. A vector image is a presentation of the content as points and lines. Do you mean translate the bitmap into Bézier curves etc? Like a desktop publishing/vector art app? That's a lot of work to achieve no useful outcome. If the issue is solving aliasing, we can just apply better AA techniques.

Anyway, this has nothing to do with framerate upscaling so I'll move this discussion to its own space.

 

[msaki]

I don't understand what you mean by 'vector image'. A vector image is a presentation of the content as points and lines. Do you mean translate the bitmap into Bézier curves etc? Like a desktop publishing/vector art app? That's a lot of work to achieve no useful outcome. If the issue is solving aliasing, we can just apply better AA techniques.

Anyway, this has nothing to do with framerate upscaling so I'll move this discussion to its own space.

vector image isnt just useful for simple points and lines it can be applied to any type of image according to the resolution

 

[Shifty Geezer]

a few years ago raytracing was deemed impossible for realtime and now we have semi pathtraced games, a billion polygons per scene where impossible until ue5 was revealed running on the ps5 with billions of triangles seamlessly, even other unusual technologies like in media molecule's dream solve things that traditional pipelines couldnt.

No, these are ideas developed over a long time, often waiting for the hardware to become fast enough or feature-rich to enable them. There was nothing innately bad about streaming geometry and Nanite didn't come out of nowhere. It was the first amazing implementation of a clear, sensible future that clever people have been looking into for a long time. Vectorisation is also something people have been looking at for 20+ years, so if it's not happening how you want, there's goimg to be a reason you'll need to understand.

Because people dared and researched it.

If you don't want this thread locked, you need to stop asserting this as your only argument in favour of your proposition. Some things are impossible, like perpetual motion machines. Here we don't take anything on faith. Discuss on a technical level what the performance needs are to turn a 2D rasterisation into a vector map and back again. Find examples of complex photos being compared this way. Put in the effort to make a logical argument rather than just repeating a belief. Thanks.

i can only see vectors solving aliasing issues otherwise its gonna be unending reconstruction techniques that will never be clearer than a vector image and also have artefcats.

Vectors cannot represent detail well. There's a good reason why the entire world has turned to AI upscaling for photographs rather than turning it into vectors. You seem to have missed the detail of the video you linked.

1) You say it should be easy to convert. "why cant game engines simply transform the final rendered frames or raster images into vectors simply since vectors are infinite it means the end of aliasing, is it really that hard nowadays"

As per the video:

"The immediate question arises - why are we not using vector graphics everywhere? Well, one, the smoother the color transitions and the more detail we have in our images, the quicker the advantage of vectorization evaporates. And two, also note that this procedure is not trivial and we are also often at the mercy of the vectorization algorithm in terms of output quality. It is often unclear in advance whether it will work well on a given input."

Vectors can't represent textures or tiny details well. Or rather they can't be extracted from low information-density sources. Indeed, in vector art apps the detailing such as brush heads is often provided by bitmaps.

2) Your example video only works on sketches.

3) Your example video literally changes the content! It takes a source that is marked as a sketch and so can interpret it and simplify it. An upscaler that changes the game's content isn't terribly useful.



Now if you're using this as 'just an example of how R&D can solve problems' and not a specific example of your upscaling idea, that's a far, far, far cry from "just using vectors, it should be easy," when the software doesn't exist yet. In that case your' saying "why doesn't someone just invent an algorithm and then make some custom hardware for it?" If you actually want that answered, you'll need to listen why your idea won't work rather than extol it as the better future. It also probably never will but for that you'd need a discussion on data representation which'd be more maths than you and I can manage. There's a reason why several decades of photo upscaling strategies has moved to AI despite past image vectorisation research and implementation, and that presents a better trajectory for game image upscaling.

Go check what the state of the art of 20 years of photo vectorisation is and then see if it really is a good and easy solution to image upscaling.

 

[Shifty Geezer]

vector image isnt just useful for simple points and lines it can be applied to any type of image according to the resolution

Your images suffer from posterisation! They look far worse than DLSS1. Vectors can't do detail. Vectors represent edges and areas which are a terribly fit for a lot of visual detail.

 

[msaki]

No, these are ideas developed over a long time, often waiting for the hardware to become fast enough or feature-rich to enable them. There was nothing innately bad about streaming geometry and Nanite didn't come out of nowhere. It was the first amazing implementation of a clear, sensible future that clever people have been looking into for a long time. Vectorisation is also something people have been looking at for 20+ years, so if it's not happening how you want, there's goimg to be a reason you'll need to understand.

If you don't want this thread locked, you need to stop asserting this as your only argument in favour of your proposition. Some things are impossible, like perpetual motion machines. Here we don't take anything on faith. Discuss on a technical level what the performance needs are to turn a 2D rasterisation into a vector map and back again. Find examples of complex photos being compared this way. Put in the effort to make a logical argument rather than just repeating a belief. Thanks.

Vectors cannot represent detail well. There's a good reason why the entire world has turned to AI upscaling for photographs rather than turning it into vectors. You seem to have missed the detail of the video you linked.

1) You say it should be easy to convert. "why cant game engines simply transform the final rendered frames or raster images into vectors simply since vectors are infinite it means the end of aliasing, is it really that hard nowadays"

As per the video:

Vectors can't represent textures or tiny details well. Or rather they can't be extracted from low information-density sources. Indeed, in vector art apps the detailing such as brush heads is often provided by bitmaps.

2) Your example video only works on sketches.

3) Your example video literally changes the content! It takes a source that is marked as a sketch and so can interpret it and simplify it. An upscaler that changes the game's content isn't terribly useful.

View attachment 8357

Now if you're using this as 'just an example of how R&D can solve problems' and not a specific example of your upscaling idea, that's a far, far, far cry from "just using vectors, it should be easy," when the software doesn't exist yet. In that case your' saying "why doesn't someone just invent an algorithm and then make some custom hardware for it?" If you actually want that answered, you'll need to listen why your idea won't work rather than extol it as the better future. It also probably never will but for that you'd need a discussion on data representation which'd be more maths than you and I can manage. There's a reason why several decades of photo upscaling strategies has moved to AI despite past image vectorisation research and implementation, and that presents a better trajectory for game image upscaling.

Go check what the state of the art of 20 years of photo vectorisation is and then see if it really is a good and easy solution to image upscaling.

ive just showed you that it doesnt only work on simple lines and sketches,

Your images suffer from posterisation! They look far worse than DLSS1. Vectors can't do detail. Vectors represent edges and areas which are a terribly fit for a lot of visual detail.

you can argue they look far worse than dlss1 but you cant say its only lines and sketches, and its not impossible as you religiously compare it to perpetual motion, you can say its expensive to do currently thats fair, raytracing was possible on a ps2 but expensive at the time and due to more performant hardware and softwaare through the years it is now possible also by the help of ml and other algorithms, i dont understand ur obsession with vectors being impossible and forever upscaling being the only solution that just sounds religious

 

[JoeJ]

The image on the right is not clearly better. The amount of detail is the same. So what's the advantage?
You can upscale the vector image, and it does not change, yes.
But that's not our problem. We try to reconstruct missing information, including adding details. This 'missing' information is often present in older frames where the pixel grid was off by subpixel amount, which is how temporal reconstruction works. It gathers the high details over time from a combination of multiple low res images.

Additionally, ML methods can also 'invent' new details which they have learned from other, similar images.

What you have in mind is likely a purely spatial upscaling, like e.g. FSR 1.0 is.
Here, there are no previous frames of temporal data, and there is no invention of new detail.
Instead, we try to turn pixelated gradients into a sharp boundary, exactly like your given Photoshop filter does.
And that's the point i think you ignore or don't know, so listen:

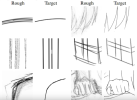
To find the sharp curve, we analyse the image and calculate things like gradients.
It works by relating the current pixel with it's neighbors. The gradient then is a vector, centered at the pixel, and it can point into the direction where brightness increases, or some color changes, etc.
This vector is quantized in position, but not in direction. The direction can be any angle at unlimited precision.
If we want a vector at arbitrary position, we interpolate surrounding vectors at this position. We may use a 3x3 region of pixels and a cubic filter, which uses the same math than various splines.
After we can do this, we can follow a gradient vector, for example until its magnitude becomes zero. We will end up at some sub pixel position which isn't quantized.
We just found one point of our curve. We repeat the search on another nearby position, and connect the found points to form a spline.

So this is how your idea works. This is how to convert quantized image data to vector data, which can be polygons or bezier patches, solid colors or gradients.

But what you should realize is: We can do this, using the exact same methods, getting the exact same final results at target resolution, without a need to deal with vector data.
I can, did, and will keep doing this in image data, simply because its much faster and easier as well.

So if you understand this and agree, then what's your point to use vector data anyway, although there is no need for it.
If you understand and don't agree, what is where i'm wrong?
If you don't understand, there's no outcome from reading papers if you're not a developer yourself to implement them. You can not invent solutions by combining random papers which sound like some good idea by belly feeling.

 

[jlippo]

ive just showed you that it doesnt only work on simple lines and sketches,

you can argue they look far worse than dlss1 but you cant say its only lines and sketches, and its not impossible as you religiously compare it to perpetual motion, you can say its expensive to do currently thats fair, raytracing was possible on a ps2 but expensive at the time and due to more performant hardware and softwaare through the years it is now possible also by the help of ml and other algorithms, i dont understand ur obsession with vectors being impossible and forever upscaling being the only solution that just sounds religious

If you want to do something similar to the posted video and replace textures with vectors, you can use vertex colors on decimated mesh.
It doesn't as is work as curved areas, but it can be made to work.

As for actually rendering it, Nanite could be interesting choice.
It will cause some popping and it would be good to reduce rendered polygon size to smaller than default.
For high contrast content antialiasing would be problem.

Not sure if there can be any advantages doing something like this. (For text and such distance fields are used to get the scaling advantage already..)

 

[Shifty Geezer]

ive just showed you that it doesnt only work on simple lines and sketches,

1) I typed that before you added the photo example.
2) Those photo upscales are terrible in preserving the qualities of the original and no use for games. She has blobby eyes, a distorted face silhouette, and decimated detail in the hat looking like the very worst and extreme texture compression.



The details are destroyed, and upscaling this will just make it look like it's been passed through a 'perturbed glass' post effect or something. Particularly because there'll probably be zero continuity between shape boundaires and they'll wobble.

Edit: Highlighting the differences of the un-upscaled source. This is how different the vectorisation is at native resolution and how much damage has been done to the source information:

, i dont understand ur obsession with vectors being impossible and forever upscaling being the only solution that just sounds religious

I've not obsessed anything. I've posted a perspective. You're the only one repeating yourself without advancing the debate on a technical level. I also haven't said it's impossible, I've said it's probably impossible - feel free to prove me wrong with technical points addressing the existing shortcomings of vector upscaling, in particular.

Elevate this discussion to something technical in your next response or it'll be locked.

 

[arandomguy]

Although I wonder if there might be an application here depending on the visual style for the game, specifically such as "toon/anime" visual style games.

 

[Shifty Geezer]

Pretty sure MS had a 2D upscaler. Googlage throws up this realtime 3ms upscaler :

https://gigazine.net/gsc_news/en/20190817-anime4k/

I imagine the processing overhead to convert to vector art and upscale is far higher than these 2D systems. If the art-style would benefit from vectorisation, it'd probably be better the art was created as 2D vector curves in the first instance and use a specific 2D vector-art engine.

There's a Sony Anime upscaler article dated 2011 on the same page.

 

[milk]

Try to reconstruct vector data from pixels (which will be faulty) why?
Rasterize the reconstructed vector data again, why rasterise again cant it just be viewed/stored as a vector image why the need to raster? ive played flash games that used vectors and had infinite resolutions no matter how you zoomed they where just clean, not much of them this days though but it is possible i just dont understand the obsession to rasterize

This made your misconceptions very clear.

Any modern display is essentially a raster monitor. It's given an array of pixels (a bitmap) and it reproduces them phisically to you.

Vector aplications like CAD software, Adobe Illustrator or an old Flash Game also rasterized their vector graphics into a bitmap and feed that to your display (with windows as a middle man compositing that aplications graphic's with the others...)

There is no such thing as "rendering vectors directly". That's an ill-defined concept that I don't believe evn you fully know what its supposed to mean. Unless you are talking about old Asteroids Arcade Cabinets.

When you pause a flash animation, and use the righ click dialogue box to zoom in, the aplication is simply re-rendering (re-rasterizing) the vectors from a zoomed out projection. That same functions can trivially be implented into any 3d game engine, the only question would be "what for?".

Both flash and 3d engines are very similar on high level. They have different primitives though. 3D engines use textured 3d triangles. Flash uses filled 2D shapes bounded by bezier curves. Both of them deal with the data in vector space untill the final step where the buffer is drawn, at which point their vector data is analysed by some algo to define the color of each pixel in the final buffer.

Flash has good AA simply because it was designed with that goal. If a game engine decides to sacrifice asset complexity for the sake of fixed Native Resolution rendering with robust analytical anti-aliasing, it technically could be possible. It will likely look like a PS2 game complexity-wise, if not worse...

 

[homerdog]

Vector aplications like CAD software, Adobe Illustrator or an old Flash Game also rasterized their vector graphics into a bitmap and feed that to your display (with windows as a middle man compositing that aplications graphic's with the others...)

Yea but what if you use the bitmap that was already created from vectors to create new vectors then rasterize them back into a bitmap. Yo dawg I heard you like vectors.

Seriously though the only use case I can think of for the OP's proposal of creating vectors from the framebuffer in realtime is if you wanted to display your game on one of those laser lightshow things. Which would be pretty cool but it has nothing to do with image quality and doesn't require re-rasterizing anything.

Shop the LaserCube WiFi, and Ultra Laser Light Show Projector

Create a mind-blowing laser show, instantly. Be a Party Hero. Transform boredom into magical social experiences. Built for iOS, Android, PC, Mac.

www.laseros.com

 

[cwjs]

Then, compute shaders were introduced, but the devs were already stuck in their pixel shader mindset, and never learned to utilize the new power bringing back all the flexibility we've lost before.
Besides some basic light binning, cluster culling, and GPU driven rendering, compute remained underutilized and not much has changed.

I still think this is ungenerous -- I feel like your complaint here is mostly aesthetic about the kind of innovations we see -- it sounds like you want to see whole new datastructures rather than equally big refinements or novel applications.

The reason why algorithms as varied as things like bvh trees and kd trees aren't been innovated is because the problem space is just smaller: "what runs at high % utilization on a super parallel machine with x amount of cache, bandwidth, etc". There have been innovations in things like bottom up bvh construction, acceleration structures to represent scenes of clusters and algorithms to evaluate them in parallel, more specific partitioning methods like froxels, etc. There's moderately active realtime rendering research (I agree there could be more) but it's not going to develop whole new algorithms very often, because a log n tree with a few less steps is not going to save the kind of MS a new technique to partition the old tree more efficiently onto the gpu can.

 

[JoeJ]

I still think this is ungenerous -- I feel like your complaint here is mostly aesthetic about the kind of innovations we see -- it sounds like you want to see whole new datastructures rather than equally big refinements or novel applications.

I don't expect new data structures but new algorithms to use them.

The reason why algorithms as varied as things like bvh trees and kd trees aren't been innovated

That's data structures, no algorithms. My critique is in parts about a general reluctance of gfx programmers to use them, but that's better now, as things like ray tracing or Nanite finally do.

because a log n tree with a few less steps is not going to save the kind of MS a new technique to partition the old tree more efficiently onto the gpu can.

I do not fully understand, but this brings me to an example i can make to express what i mean:
Imagine we want to resolve lighting for every triangle in a scene. To do so, we integrate every other triangle to the current, and we also need to iterate all triangles to see if they occlude the sight from the current to the other.
So in total we have a time complexity of O(N^3) for that given brute force solution.
Me: 'Let's introduce LOD to speed things up! Too bad current RT APIs do not allow to do so.'
Other dev: 'But it's not even necessary to have LOD. Tracing a ray with BVH is O(log n), so using LOD to reduce some tree levels will not give a big speed up.'

That's probably not what you have meant, but i remember this discussion from this forum.
The other dev was focused on the cost of RT and missed to look at the whole problem, which would reduce to O((log n)^3), which is a lot actually. I'm not ungenerous, because i talk about speed ups of multiple orders of magnitude in practice.

Excuse the trivial / obvious example, but that's how it looks from my perspective. I have reduced this given problem to (practically) O(N), so the current solutions look ridiculously expensive to me, and i still call them 'brute force'.
That's where my rant comes from. I see that i sound disrespectful, but it's not meant like that. Just give me some more time to proof my point.

 

[JoeJ]

I imagine the processing overhead to convert to vector art and upscale is far higher than these 2D systems. If the art-style would benefit from vectorisation, it'd probably be better the art was created as 2D vector curves in the first instance and use a specific 2D vector-art engine.

Gives me some nostalgic vibes on former work as 2D artist. I made cartoon drawings with pencil on paper, but then used vector tools similar to Adobe Illustrator to redraw the scanned lines fixing jaggy and imperfect drawings.
Splines are better than bitmaps for this, because they allow to redraw with a small count of control points, and you can change the curves afterwards. But it had to be done all manually. Fixing automatically generated splines was much slower.

It's interesting how printed media works. The digital format is postscript, which supports bitmaps, but uses Bezier curves for vector shapes, mostly all fonts.
The vectors are then rasterized to film as solid pixels. The resolution is about 3000 pixels per inch, so that's what we would need to get rid off a need for anti aliasing. You can't see those little pixels on printed text anymore.
Though, maybe those 3000 dpi is more than needed for that. The halve tone dots to mix colors are constructed from a square of maybe 30x30 pixels, requiring some extra resolution. Computer printers have only something like 300dpi, with pixels still hardly visible.

Some wiki image showing the dots and how mixing colors works:

A pixel from a bitmap image likely uses many of those dots.
But if vectors are used, e.g. a font letter which is not black but colored, the dots are actually cut in half at the boundary, precisely following the vector shape.
So there are actually two resolutions going on. One high for solid pixels, and one low to form the dots enabling color mixing.
The dots are visible to the bare eye if we look close, but the pixels are not. So it depends a bit on the color mix how sharp a vector shape can actually be.
Because we can not assume mechanical printing always has exact alignment of the 4 usable colors, artists must be careful with small colored text.

In printed media, the mindset 'vectors > bitmaps' is very common. But for a different reason: If you have some logo for your company, you want it in vectors. Because you will need it in variable sizes over time. You'll use it in small printed announcements, but also on huge posters. So if you have it in vectors, you don't need to worry about artist complaints like 'your bitmap logo will look pixelated on the poster'.

This still holds for something like websites.
But in games or movies it doesn't. We always know in advance what our output resolution will be, and we also know our upscaling factor won't be more than 2 or a crazy 4 at most.
Even if we had 3000 dpi displays, we would not rasterize to bitmaps, generate vectors from the bitmap, and rasterize again at higher resolution.
But we could (and already do) use a similar method as in print: Rasterize at high resolution, but do costly stuff (SSR, AO, any lighting) at lower resolution and try to upscale that so it fits.