MENSA triangle riddle

[London Geezer]

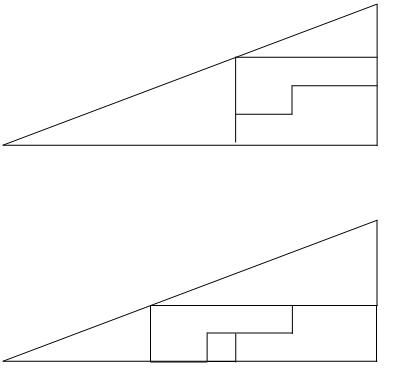
Yes you are right the red and green are not similar.

Your previous post was ambigious, I thought you meant the two red, likewise for green, triangles are not congruent.

Well the test itself says that the figures in the first big shape are the same as the ones making up the second one, so yeah the red triangle is congruent to the second red triangle, and all the other shapes too with each other.

And... i can't believe i remember this sort of stuff from school...

 

[K.I.L.E.R]

Did anyone notice that there are triangles that aren't triangles?

 

[London Geezer]

Did anyone notice that there are triangles that aren't triangles?

Yes, also pimples that are really black spots.

 

[Andy]

I'm not sure if the slope of the "triangles" really matters. Has anyone tested this on paper? Say you draw a real triangle 5 units high by 13 units long and of course the hypotenuse is square root of 194 (or 13.93 to 2 decimal places), then draw and cut out the shapes, are you still able to recreate the second triangle from the shapes of the first triangle?

I tested this in word, and I don't see any real difference between the sloped and normal triangles :

 

[RussSchultz]

The shape/ratio of the internal triangles is the whole key.

In one configuration, the area of the quadrilateral (because that's what the 4 shapes put together form--there's 4 corners) is 1 unit larger than the other configuration.

 

[Andy]

I came to the same conclusion, the 2nd triangle is actually slightly larger than the first, and in that slightly larger space that youve gained in the 2nd triangle is where the missing square lays hidden

The total area hasnt changed, it's just been shuffeled around a bit.

 

[Crisidelm]

Same ol' same ol'...

 

[Crisidelm]

I came to the same conclusion, the 2nd triangle is actually slightly larger than the first, and in that slightly larger space that youve gained in the 2nd triangle is where the missing square lays hidden

The total area hasnt changed, it's just been shuffeled around a bit.

As RussSchultz hinted (Ok, he said it fair and square): are THOSE triangles?

 

[Simon F]

As RussSchultz hinted (Ok, he said it fair and square): are THOSE triangles?

Well, the bottom figure clearly isn't. It's got a hole in it

 

[K.I.L.E.R]

The total area hasnt changed, it's just been shuffeled around a bit.

Hence why the orange and green blocks are unique.
It's because of the arms which are extended when they are shifted that cause the stupid white square.

 

[Crisidelm]

As RussSchultz hinted (Ok, he said it fair and square): are THOSE triangles?

Well, the bottom figure clearly isn't. It's got a hole in it

That's the point: I keep reading about people talking about the "two triangles"

 

[Andy]

Okay would you rather I said Figure 1 and Figure 2 are "Triangularesque"

 

[RussSchultz]

Okay would you rather I said Figure 1 and Figure 2 are "Triangularesque"

Further hint: the "hypotenuese" in figure 1 and figure 2 is not a straight line.

 

[Crisidelm]

Okay would you rather I said Figure 1 and Figure 2 are "Triangularesque"

anyway, it's one of the two "infamous" mind riddles that pop out every now and then: this and the notorious "Einstein said only 2% of world population can solve it" one. Don't know how many times I've seen it already...

 

[Andy]

Okay would you rather I said Figure 1 and Figure 2 are "Triangularesque"

Further hint: the "hypotenuese" in figure 1 and figure 2 is not a straight line.

I already acknowledged that if you bothered to read my first post, but if you look at the pictures I posted you will notice that it doesnt seem to matter if the "lines" on the triangle are curved or straight

 

[TekkenMaster]

If you can't solve the riddle that "Einstein said only 2% of world population can solve it" does it make you popular?

By the way, what is that riddle?

 

[London Geezer]

If you can't solve the riddle that "Einstein said only 2% of world population can solve it" does it make you popular?

By the way, what is that riddle?

Well it's normal, we all know that 98% of the people out there are stupid.

 

[RussSchultz]

I already acknowledged that if you bothered to read my first post, but if you look at the pictures I posted you will notice that it doesnt seem to matter if the "lines" on the triangle are curved or straight

Again, it isn't a triangle. The "hypotenuese" isn't curved, its got two segments, making in both cases, a quadrangle.

The key is that ratios of the legs of the two triangles aren't the same. (one is 5:2, the other is 8:3) Depending on which way they're stacked, the two hypotenueses of the two triangles will form either a concave, or a convex line segment.

In the first configuration, the "hypotenues" is formed by a concave pair of segments. In the second configuration it's a convex pair of segments. If we ignore the notch formed, and assume the bottom leg is solid, we can calculate the area of the two quadrangles.

You'll find that the concave quadrangle (top one) is 1 unit smaller than the convex "quadrangle" (bottom one).

 

[London Geezer]

This riddle was solved in the first page, if anyone missed that....

 

[Zaphod]

if you look at the pictures I posted you will notice that it doesnt seem to matter if the "lines" on the triangle are curved or straight

No. Not curved at all. Just not straight. Allow me to exaggerate:

Edit: Russ beat me to explaining it perfectly well without the need for visual aides... 8)