Can a 4x4-Filter produce better quality than common TF?

[aths]

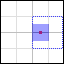
This image should be used for a particular example. Every Quad is a Texel, the red dot a specific sample position. Well, trilinear filtering is a linear interpolation of 2 bilinear samples.

The first bilinear sample is calculated by putting a kernel with side length = 1 texel around the sample. In this case, only 2 texels are used. (The hardware filters 4 texels for every sample, the 2 unused texels are weighted with 0, the other texels with 0.5.)

The other sample is from a mip map 1 level higher. To create this mip map, in most cases a simple 2x2-blockfilter is used. To underline this effect, I emphases this blocks with stronger lines.

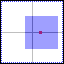
We got an effect of a "displacement-error". The new kernel is still centered arount the sample. But at the left hand are more contributing texels than on the right hand. This results from the pre-filtering of the mip-map.

Its evident, that a 4x4-Filter can filter trilinear from one mip-map (look at the image above.)

The question is, is a 4x4-Filter limited to common trilinear quality, or can an even "better" (more realistic) pixel color produced?

 

[Simon F]

Aths,
If you assume a box filter has been used to produce the lower map levels then it's OK, however, some applications may use better filter kernels (eg Bartlett or Gaussian) to produce the lower level maps.

 

[aths]

Yes I do premise a 2x2 block filter for mip-map generations. Imo, there are good reasons against gaussian or other types, but "alternative" mip-map generation filters are not my concern here.

Can be filtered more "realistic" trilinear with putting a 3x3-kernel around the sample?

If so, how to calculate the weight-matrix? LOD fraction should be an important parameter for this matrix, but how to apply?

My approach is, to extend from bilinear (with kernel-width of 1 texel) to "one mip-map-level lower" bilinear (with a kernel-width of 2 texels, and thereforce a 3x3-kernel to be free to place the 2x2-box everywhere.) Its now possible to generate a weight-matrix to simulate an interpolation of the "real" bilinear texel and the "one mip-level lower" bilinear texel.

If this thread is correct, even a 3x3 filter can produce better quality than common trilinear filtering. Another advantage: The bandwidth cost is only marginal higher than common trilinear, while a 4x4-filter consumes much more bandwidth.

 

[psurge]

aths - but a 4x4 filter kernel should have a higher cache hit rate than tri-linear (more overlap in required samples).

Regards,
Serge

 

[tjl]

Can be filtered more "realistic" trilinear with putting a 3x3-kernel around the sample?

If so, how to calculate the weight-matrix? LOD fraction should be an important parameter for this matrix, but how to apply?

Hey, bilinear and trilinear *are* really bad. Look at the literature for e.g. Heckbert and EWA to understand how far in the other direction you could go.

 

[KimB]

The main reason for using better than trilinear filtering is for magnified textures. Current trilinear coupled with anisotropic filtering really is excellent for minification, but magnification is where things need work.

And using a 4x4 filtering is usually termed bicubic, since a cubic fit to four samples is used. The main cost when doing bicubic filtering isn't the memory bandwidth hit, as texture cache hits are much higher. It's the processing hit.

But bicubic filtering is relatively wasted anyway when texels are about a pixel in size. When magnifying, however, trilinear filtering is prone to producing very blocky texels. Bicubic does a much better job, and would therefore be much better suited to filtering of magnified textures such as lightmaps.

 

[Mintmaster]

I don't think using 4x4 necessarily implies using a bicubic filter. After all, in signal theory the sinc function is the ideal reconstruction filter. You could do a convolution with part of a sinc function that spans a larger grid(renormalized, of course), but there could be some ringing artifacts if the texture isn't properly made. This would be much more mathematically feasible.

However, I think you're right in that a bicubic filter is generally accepted as the best quality you can get doing magnification.

 

[Mintmaster]

double post.

 

[Simon F]

And using a 4x4 filtering is usually termed bicubic, since a cubic fit to four samples is used.

Not at all. The cubic refers to the shape of the curve but there's nothing to stop you taking a different number of taps.

 

[OpenGL guy]

Its evident, that a 4x4-Filter can filter trilinear from one mip-map (look at the image above.)

This is not new. The Savage 3D could do this in ~1997-8

 

[Rolf N]

Whatever the implementation looks like, I'd love to see single cycle trilinear in next gen hardware. Maybe the time for bilinear is just over. 'Legacy' titles should be fast enough (TM) and would get a little extra quality forced on them. Fragment shading heavy titles would be rather limited by execution, not filtering, methinks, so trying to wring extra speed by making bilinear faster than trilinear doesn't make a whole lot of sense anymore, IMO.

*stares at OpenGL guy*
*hinthint*

Much preferred over dedicated hardware support for brilinear hackery. I smell a competitive advantage waiting to happen

 

[zsouthboy]

Whatever the implementation looks like, I'd love to see single cycle trilinear in next gen hardware. Maybe the time for bilinear is just over. 'Legacy' titles should be fast enough (TM) and would get a little extra quality forced on them. Fragment shading heavy titles would be rather limited by execution, not filtering, methinks, so trying to wring extra speed by making bilinear faster than trilinear doesn't make a whole lot of sense anymore, IMO.

*stares at OpenGL guy*
*hinthint*

Much preferred over dedicated hardware support for brilinear hackery. I smell a competitive advantage waiting to happen

But then you can't do the brilinear thing yourself, to get that extra bit of speed, since your competitor is doing it.

I too would love to see 1 cycle trilinear. Please? However, in the grand scheme of things, its not THAT important. I'll take my 500 fps in Q3 now, thankyouverymuch.

 

[KimB]

I don't think using 4x4 necessarily implies using a bicubic filter. After all, in signal theory the sinc function is the ideal reconstruction filter. You could do a convolution with part of a sinc function that spans a larger grid(renormalized, of course), but there could be some ringing artifacts if the texture isn't properly made. This would be much more mathematically feasible.

But, if I remember correctly, a sinc function requires you to sample over the entire texture. That's not exactly feasible, and I doubt it would produce good results if you approximated it with a 4x4 sample pattern.

Bicubic is perfect for 4x4 because four samples uniquely determine a cubic function. Of course, there are a couple of different ways you can produce the cubic function (I think the best is to fit the value of the cubic function and its first derivative at the two nearest sample points, instead of having the cubic function go through all four sample points).

What may be about the best we can hope for going into the future is a 4x triilinear + bicubic + anisotropic filtering method. This method would always sample either bicubic, or at least four trilinear samples (two trilinear samples in each direction). More trilinear samples would be taken in any direction that needs it (anisotropic filtering). Bicubic would be used for magnification, and anisotropic for whenever two samples isn't enough to properly display the base texture in any one direction.

 

[Rolf N]

<...>
Much preferred over dedicated hardware support for brilinear hackery. I smell a competitive advantage waiting to happen

But then you can't do the brilinear thing yourself, to get that extra bit of speed, since your competitor is doing it.

Part of my point, actually.
You not only remove the burden of trying to detect any filtering hacks from the press (if any), because you technically can't gain anything, you also remove the temptation to implement them

I too would love to see 1 cycle trilinear. Please? However, in the grand scheme of things, its not THAT important. I'll take my 500 fps in Q3 now, thankyouverymuch.

Speed, huh? That's what this is about, of course
All I'm trying to say is that keeping bilinear "fast" in exchange for trilinear being "not as fast" (up to 50% fillrate loss in pathological cases) is, essentially, a diminishing benefit for older apps that aren't much affected by shader execution. Even so, they are fast enough already on current hw.

And, of course, it's a particularly easy way to make it 100% clear that you're not cutting corners on texture filtering. This should be a huge relief for anyone trying to wrap their minds around Intellisample

 

[tjl]

The main reason for using better than trilinear filtering is for magnified textures. Current trilinear coupled with anisotropic filtering really is excellent for minification, but magnification is where things need work.

This is *so* not true for sharp edges. When using fonts, using 4x texture supersampling in the fragment pipeline like this (works on NV3X; load a texture into the texunit 0 and (IMPORTANT) use LOD bias -1, to use a more accurate version of the mipmap. It doesn't start aliasing because we take 4 samples spaced correctly):

!!FP1.0
DDX H0, f[TEX0];
DDY H1, f[TEX0];
MAD H0, H1.xyxy, {1,1,-1,-1}, H0.xyxy;
MUL H0, .25, H0;
ADD R0, H0, f[TEX0].xyxy;
TEX H1, R0.xyxy, TEX0, 2D;
TEX H2, R0.zwzw, TEX0, 2D;
ADDX H2, H1, H2;
MULX H2, H2, .25;
ADD R0, -H0, f[TEX0].xyxy;
TEX H0, R0.xyxy, TEX0, 2D;
TEX H1, R0.zwzw, TEX0, 2D;
ADDX H0, H0, H1;
MADX o[COLH], H0, .25, H2;
END

yields a LOT less blurry result. Can't be bothered to make screenshots right now; am writing a paper about some other related stuff, will be included there.

Of course, it's not as much a difference as between anisotropic filtering and no anisotropic filtering in aniso situations, but it's still a huge difference when you want to render smallish text legibly.

(edit: remember to mention lod bias, without it the code just blurs the texture

 

[bloodbob]

Not quite a 4x4 but a 3x3

http://www.vrvis.at/vis/research/hq-hw-mipmap/ the interesting thing they pointed out that I didn't know was need the blending of the mip maps has to be modified to produce the correct image but I'm sure 1/2 of you knew that.

 

[Xmas]

tjl, you could save one instruction, or even two if you allow the grid to be displaced 1/4 pixel in one or both axes
Don't know if it would be faster, though...

 

[tjl]

tjl, you could save one instruction, or even two if you allow the grid to be displaced 1/4 pixel in one or both axes
Don't know if it would be faster, though...

How? I actually calculate the 4 offsets in parallel using a 4-vector as 2x2, I don't see how I could get by with less instructions. OTOH, it's late and I might be missing something...
:?

 

[Xmas]

!!FP1.0
DDX H0, f[TEX0];
DDY H1, f[TEX0];
  1    MAD H0, H1.xyxy, {1,1,-1,-1}, H0.xyxy;
       MUL H0, .25, H0;
       ADD R0, H0, f[TEX0].xyxy;
TEX H1, R0.xyxy, TEX0, 2D;
TEX H2, R0.zwzw, TEX0, 2D;
ADDX H2, H1, H2;
MULX H2, H2, .25;
  2    ADD R0, -H0, f[TEX0].xyxy;
TEX H0, R0.xyxy, TEX0, 2D;
TEX H1, R0.zwzw, TEX0, 2D;
ADDX H0, H0, H1;
MADX o[COLH], H0, .25, H2;
END

You're trying to sample at the positions
f[TEX0] + 0.25 *(ddx(f[TEX0]) + ddy(f[TEX0]))
f[TEX0] + 0.25 *(ddx(f[TEX0]) - ddy(f[TEX0]))
f[TEX0] + 0.25 *(-ddx(f[TEX0]) + ddy(f[TEX0]))
f[TEX0] + 0.25 *(-ddx(f[TEX0]) - ddy(f[TEX0]))

But you could also take:
f[TEX0]
f[TEX0] + 0.5 * ddx(f[TEX0])
f[TEX0] + 0.5 * ddy(f[TEX0])
f[TEX0] + 0.5 * (ddx(f[TEX0]) + ddy(f[TEX0]))


Replace the indented lines with either of the following:

Grid displaced 1/4 pixel in x- and y-axis:

1  MAD R0, H0.xyxy, {0, 0, 0.5, 0.5}, f[TEX0].xyxy;

2  MAD R0, H1.xyxy, { 0.5, 0.5, 0.5, 0.5}, R0;

Grid displaced 1/4 pixel in y-axis:

1  MAD R0, H0.xyxy, {-0.25, -0.25, 0.25, 0.25}, f[TEX0].xyxy;

2  MAD R0, H1.xyxy, { 0.5, 0.5, 0.5, 0.5}, R0;

Grid not displaced:

1  MAD R0, H0.xyxy, {-0.25, -0.25, 0.25, 0.25},  f[TEX0].xyxy;
   MAD R0, H1.xyxy, {-0.25, -0.25, -0.25, -0.25}, R0;

2  MAD R0, H1.xyxy, { 0.5, 0.5, 0.5, 0.5}, R0;

 

[OpenGL guy]

I too would love to see 1 cycle trilinear. Please? However, in the grand scheme of things, its not THAT important. I'll take my 500 fps in Q3 now, thankyouverymuch.

How does this 4x4 trilinear filter work with AF? Not very well...

What you fail to realize is that taking 16 texture samples at once is very difficult. You need to have a lot more interpolators (4x as many than if you just wanted full-speed bilinear).