my professor put the final exam grades in on wednesday. i got 132/200... a 66%...
...but i still ended up with a 78 overall. i passed calc i.
Congratulations!
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
my professor put the final exam grades in on wednesday. i got 132/200... a 66%...
...but i still ended up with a 78 overall. i passed calc i.
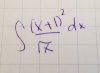
Work is described as being force applied over a displacement. In terms of units, it is measured in Joules, which are Newton*meters, which are kg*m/s^2 * m = kg*m^2/s^2.
Just from the equations, there is a lack of agreement in units if g is not included.
W needs to be have quantities of meters, kilograms, and seconds.
W (kg*m2/s2) = 2m^2 * delta y m * 9.8(m/s2) * 1000 kg/m^3 * (1-yi)m
Without g, it is immediately obvious there is is no s^-2, and so no Joules.
Next, getting the mass of water from kg/m^3 cancels out too many units of length to give the necessary m^2 in kg*m^2/s^2.
As an attempt to give a reason outside of the equation itself, one thing to look at is what is being calculated, or how it is treated in experiments. Usually, scenarios in physics where objects are being lifted against gravity are going for a minimum amount of work needed to lift the mass a given distance. In that case, there is an attempt to apply an upward force sufficient to get the mass moving up, but at a constant velocity from t=0 to the end of the time interval.
No acceleration means no net force, meaning any force applied is counterbalanced by gravity. The work the lifter performs can be calculated in terms of the known mass and acceleration due to gravity that has been perfectly matched.
There was an initial acceleration or excess force, although that can be excluded if measurement starts after, and in a theoretical setup can be an amount of excess force that can be arbitrarily reduced towards zero. (Newton's 2nd Law, an object's motion will not change in the absence of a net force.)
In the absence of gravity, that trivial initial bit of force that can be reduced arbitrarily close to zero would be able to give the same displacement as a pump laboring against the acceleration due to gravity.
Since work is force over distance, a lack of gravity means force goes to 0, and so essentially no work is necessary to lift the water. In the problem scenario, there is force applied to continually keep gravity from accelerating the water downwards, and it is applied over the vertical displacement.
Why this is useful comes when asking how much gravitational potential energy is in this system due to the water being raised, which would also be the amount kinetic energy measured if the water were allowed to fall back to the initial level. The quantities of energy are not coincidentally measured in Joules. A change in the amount of energy in a specific system, or a transformation of energy from one form or another is known as work.
also hey. to anyone. i had my first calc ii exam and this integral is stuck on my mind. everything i saw via calculators showed it ending up with like... stuff on the numerator with 5 as the denominator. im too lazy to pull out any of the chicken-scratch work i tried doing afterwards, but... what the FUCK is this integral?
If someone tries to talk to you about quantum mechanics - RUN..............i really need to understand how physics work better.
