Question about a quote from the B3D G80 article, and nvidia FUD doc

[Techno+]

Hello,

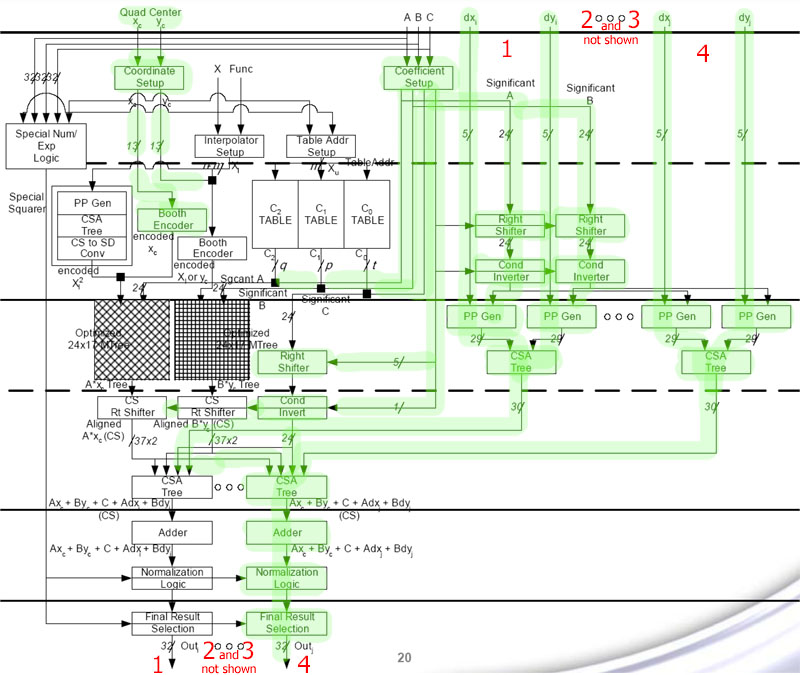
While I was going through the B3d G80 tech article I came across this

Attribute interpolation for thread data and special function instructions are performed using combined logic in the shader core. Our testing using an issue shader tailored towards measuring performance of dependant special function ops -- and also varying counts of interpolated attributes and attribute widths -- shows what we believe to be 128 FP32 scalar interpolators, assigned 16 to a cluster (just as SPs are).

from the nv FUD

Geforce 8800 has 128 standard ALUs and 128 SFUs

I'm confuses, the B3D article says the SF operations are done on the shader cores, while he nv FUD doc says it has 128 SFU for SF operations. I'm sure that both are correct, and that I have missed something out, can you point it out and eplain?

Thanx a lot

 

[Jawed]

The SF ALU in G80 can produce 1 SF per clock (erm, depends on the instruction, some SFs are 1 every 2 clocks).

Because the SF is also the interpolator, it can produce 4 scalar attribute interpolations per clock.

So, each SF in theory can also do 4 MULs. This is the origination of the idea that G80 is MAD+MUL. Except, ahem...

Jawed

 

[Techno+]

The SF ALU in G80 can produce 1 SF per clock (erm, depends on the instruction, some SFs are 1 every 2 clocks).

Because the SF is also the interpolator, it can produce 4 scalar attribute interpolations per clock.

So, each SF in theory can also do 4 MULs. This is the origination of the idea that G80 is MAD+MUL. Except, ahem...

Jawed

So the normal shader ALUs, which are already exposed, contribute to the MADD, while these SFUs, which aren't currently exposed, contribute to the MUL. And these SFUs are the "proposed FP functional unit"? right?

Thanx a lot

 

[Jawed]

So the normal shader ALUs, which are already exposed, contribute to the MADD,

Yes.

while these SFUs, which aren't currently exposed, contribute to the MUL. And these SFUs are the "proposed FP functional unit"? right?

Yes. SFU splits the interpolation into two parts for 4 pixels in parallel. The most significant part is handled as a common operation on an the "centre" of those 4 pixels.

The pipeline stages to perform this "most significant" calculation are also used to produce a SF (reciprocal, sine, etc.) based on look-up tables. This is why the SF can only produce one result per clock.

Separately, there are 4 paired math pipelines. Each pair performs the 2D interpolation (x,y) on the least significant bits.

So, when this unit is asked to perform interpolation, it combines the calculated interpolation for the "4-pixels centre" with the four low-precision interpolations to produce a final scalar value for the 4 pixels.

In theory, these 4 "least significant" pipelines can do MUL. But in reality their precision is not enough for fp32 MUL. The only way they could be used as MUL, as far as I can tell, is to use one at a time in combination with the "pixel centre" most-signifcant stages. This would then produce 1 MUL.

So in this way you could call G80 MAD+1/4MUL. This may be the reason why some SFs take 2 clocks per result, because the first clock is spent performing a high-precision MUL. Dunno...

Jawed

 

[Techno+]

thanx a lot. Your info is of great help.

 

[silent_guy]

Yes. SFU splits the interpolation into two parts for 4 pixels in parallel. The most significant part is handled as a common operation on an the "centre" of those 4 pixels.

It's not exactly clear to me what is being interpolated when.

Here's what I understand: Ignoring the GS, at the output of the VS, you will get a triangle that needs to rasterized into individual pixels. For each vertex, there is a bunch of vertex attributes. You need to interpolate between those 3 vertices to get the attribute value per pixel. I would think that this is not something you would do here, because you can probably calculate those values by calculating dAttr/dx, dy, dz once and then just step them for each pixel, so no need for a multiplication. Is this right?

So what is this interpolation then used for? Has it to do with textures? Converting from x,y,z space to s,t texture coordinates? Other usage? Will this happen in the VS or PS or both?

(I seem to remember some discussion that say that this was done in a separate unit on G70 or R520?)

Does that mean that those interpolation instructions are explicitly coded by a shader programmer or is this something that's automatically inserted by the driver when a meta-instruction (like a texture fetch?) is part of the shader program?

 

[Rys]

Does that mean that those interpolation instructions are explicitly coded by a shader programmer or is this something that's automatically inserted by the driver when a meta-instruction (like a texture fetch?) is part of the shader program?

You ask for interpolated attributes in your shader programs via the input/output semantics, although the driver should compile them out if you ask for them and don't use them. You've got access to things like colour, normal, texcoords, position there, and you can adjust the interpolation function if you need to.

It'll happen in VS and PS, depending on what you ask for.

 

[silent_guy]

You ask for interpolated attributes in your shader programs via the input/output semantics, although the driver should compile them out if you ask for them and don't use them. You've got access to things like colour, normal, texcoords, position there, and you can adjust the interpolation function if you need to.

It'll happen in VS and PS, depending on what you ask for.

I see: so in hardware, the rasterizer will only calculate the minimal parameters that are needed to later calculate the actual attribute value.

Looking at the schematic above, those minimal parameters would be A,B,C (per attribute plane equation parameters?), Xc and Yc (location of the center of the quad in the plane?) and (dx1,dy1), ..., (dx4,dy4): relative distance of the actual pixel positions from Xc and Yc.

Each attribute (s, t, r, g, b etc.) will have its own set of A,B,C parameters, constant for a complete triangle. And all x,y are constant per vertex or per pixel.

Thanks!

 

[Jawed]

In ATI hardware there's a dedicated functional block called "shader pipe interpolators" that does this.

When is this scheduled, erm, not sure. There's a theory that all interpolations are performed (per fragment) and the results stored in "constant" memory just as the batch is created. These "constants" are then fetched as required while the shader executes. It's worth noting that the amount of time required, per fragment, to perform all interpolations can vary hugely. So how this affects scheduling, and how much latency it introduces, is unknown.

Historically it seems ATI GPUs have long had a large block of memory for constants. In contrast NVidia GPUs had none. Attributes were calculated on demand and constants were treated as literals in shader code, requiring resubmission of the shader if any constant changed for some reason (e.g. the colour of lights changed).

G80 has a 64KB constant cache. In theory, I suppose, attributes could be interpolated at the start of the shader and put in the constant cache (hmm, would prolly run out of constant cache ratehr quickly). Or, at the very least, kept as normal temporary registers (hmm, there's not much space for registers in G80).

There is an NVidia patent that uses the texturing destination-register (e.g. "TEX r5 ...") to hold the parameters for the texturing pipeline to use. This could imply that attribute interpolation can be performed sooner than "just in time" but I dunno.

Anyway, a key point about G80's ALU pipeline is that interpolation creates an additional "hazard" for the compiler to deal with.

Jawed

 

[Nick]

This is the origination of the idea that G80 is MAD+MUL.

This got me thinking... Would it be possible to add some more lookup tables to the SFU so it can actually perform accurate MUL or ADD as a 'special-function' using the same logic?

As far as I know the current idea was that the SFU's can perform a co-issued MUL, but only of limited precision.

 

[Jawed]

This got me thinking... Would it be possible to add some more lookup tables to the SFU so it can actually perform accurate MUL or ADD as a 'special-function' using the same logic?

As far as I know the current idea was that the SFU's can perform a co-issued MUL, but only of limited precision.

As far as I can tell, the SF unit can already perform an fp32 MUL. It can do this as a combination of one of the "5-bit" interpolation pipelines with the booth-encoded multiplier in the SF pipeline.

I don't think it would need any change in the lookup tables, because those tables are solely for the SFs.

So, the SF unit can produce a MUL at 1/4 rate, exactly the same rate as it performs SFs (well, some of them, anyway - some are half that speed).

For ADD, I don't know. There are adders in there (limited precision it seems), but well I'm out of my depth. Also, you might argue that 1/4-rate ADD is of very little use, much less so than 1/4-rate MUL. This is because it's fiddly to co-issue into the SF unit, because the slower throughput clashes with instructions you want to issue on the MAD ALU. It does work, obviously, but it's a bit of a hazard too.

As I said in the other thread, this brings up the intriguing prospect of what happens in the double-precision "refresh" of G80. Will the lookup tables be increased in size, along with the multipliers? Or will G80 revert to performing iterative SFs when a DP result is required.

A DP divide in AMD's K8 takes 74 cycles

http://www.realworldtech.com/page.cfm?ArticleID=RWT051607033728&p=6

I'm not familiar enough with CPUs to know the latency profile of all the common DP operations, but it seems unlikely to me that DP-G80 would go fully iterative. Maybe it would use the SP result as the seed for iterative refinement?

Otherwise, I imagine the DP-SF lookup tables will end up ginormous.

Maybe there's some relevant patent applications out there, I haven't looked so far.

Jawed

 

[trinibwoy]

A DP divide in AMD's K8 takes 74 cycles

http://www.realworldtech.com/page.cfm?ArticleID=RWT051607033728&p=6

Thanks for the link!

 

[Nick]

As far as I can tell, the SF unit can already perform an fp32 MUL. It can do this as a combination of one of the "5-bit" interpolation pipelines with the booth-encoded multiplier in the SF pipeline.

But isn't that only a 17 bit multiplier?

So, the SF unit can produce a MUL at 1/4 rate, exactly the same rate as it performs SFs (well, some of them, anyway - some are half that speed).

Could you elaborate that for me please? I wondered about that 1/4 rate here as well.

A DP divide in AMD's K8 takes 74 cycles

If you can live with a few ulp error you can use the approximate reciproque instruction and a few Newton-Rhapson iterations. It's still way slower than what could be achieved with a well designed SFU though.

I'm not familiar enough with CPUs to know the latency profile of all the common DP operations...

They're the same as single-precision, except for division and square root. The x87 transcendentals are microcoded and they depend on a control word for how many accurate bits are computed.

Otherwise, I imagine the DP-SF lookup tables will end up ginormous.

Not necessarily. A while ago I wrote some exp and log approximations for the CPU using minimax with polynomials of higher degree. Based on that I'm guessing that they could keep the lookup tables roughly the same size if they use a polynomial of degree four. This translates to requiring more multipliers and adders, and likely doubling the pipeline length, but it could spew out a double-precision result every clock cycle within reasonable area cost.

 

[Jawed]

But isn't that only a 17 bit multiplier?

24-bit multipliers in the main SF path. There's two of them, actually. Do you have the PDFs, I can email them if you like - PM me. It'd be easier than me getting in the way, interpreting stuff.

You've now made me wonder about exponent processing. There is a separate path in the SF for exponent handling - it's an area I didn't really pay attention to, so I have to admit I'm now wondering if the SF can truly produce an fp32 MUL - but I think it really must do.

Arun/Rys report 1.15 MULs per clock, which implies sub-theoretical 1.25 MULs per clock being achieved in the SF unit.

Could you elaborate that for me please? I wondered about that 1/4 rate here as well.

The SF unit has, I think, 10 cycles of latency (I think I saw this in a related patent document, but I don't seem to have saved it).

If you read the PDFs carefully, you'll see that the throughput of the SF unit is 1 per cycle. The reason that SF's run at 1/4 rate is that for every 8 MADs in parallel, there's only 2 SF ALUs.

Since each SF can also interpolate the 4 pixels in a quad, it turns out that for every 8 MAD you get 8 interpolated-attributes.

You should also get the CUDA reference guide

http://developer.download.nvidia.com/compute/cuda/0_81/NVIDIA_CUDA_Programming_Guide_0.8.2.pdf

which reveals lots of extra detail about the clocking etc. (including the list of SFs that take 2 clocks).

Not necessarily. A while ago I wrote some exp and log approximations for the CPU using minimax with polynomials of higher degree. Based on that I'm guessing that they could keep the lookup tables roughly the same size if they use a polynomial of degree four. This translates to requiring more multipliers and adders, and likely doubling the pipeline length, but it could spew out a double-precision result every clock cycle within reasonable area cost.

Well, you're clearly a man of distinction. Last assembly code I wrote was PDP-8 in about 1985 - I have fond memories of 6502 machine code (never had an assembler ).

Anyway, the NVidia SF interpolation described in the PDFs is pretty interesting, specifically because of the analysis used to construct the lookup tables. The ATI SF units are also very interesting:

Technique for approximating functions based on lagrange polynomials

Method and system for approximating sine and cosine functions

When you're done, I'd be interested in your analysis of the lookup table sizes required to produce fast DP results!

Jawed

 

[Bob]

you can probably calculate those values by calculating dAttr/dx, dy, dz once and then just step them for each pixel, so no need for a multiplication. Is this right?

That would be a fine algorithm if you were rasterizing and drawing single fragments at a time. In fact, that's what GPUs used to do once upon a time.

It just happens that more modern GPUs tend to work on more fragments at a time, and thus need to be able to interpolate, in parallel, a whole bunch of attributes times a whole bunch of fragments. If you've computed dAttr/dx, then you need a MAD to obtain the value at some arbitrary x.

 

[Jawed]

I'm wondering, now, whether the SF's multiplier, on its own, is enough to produce an fp32 MUL. i.e. forget about combining the result of one of the four interpolator paths.

Jawed

 

[Nick]

24-bit multipliers in the main SF path. There's two of them, actually. Do you have the PDFs, I can email them if you like - PM me.

I have the ARITH17 slides (in PDF format), if that's what you mean. Anyway, I think I know where my confusion came from: they use a Booth encoded multiplier.

The reason that SF's run at 1/4 rate is that for every 8 MADs in parallel, there's only 2 SF ALUs.

Oh, I think I get it. One SFU can compute interpolants for a whole quad at once (there are only small gradients within a quad), while when used for special functions it can only compute one at a time.

I previously thought the 128 stream processors had one MAD unit and one (whole) SFU each. But it's really 8 MAD units sharing 2 SFU's, right? So it takes 4 clock cycles to execute a special function for all eight stream processors.

This puzzles me about the 518 GFLOPS for G80 at 1.35 GHz that floats around in some places. Is this simply incorrect? Also, doesn't this make the possibility of performing a MUL on the SFU's nearly insignificant? You'd need a shader with lots of muls and little special functions and interpolants. And even then you can 'only' gain 12.5% in GFLOPS.

which reveals lots of extra detail about the clocking etc. (including the list of SFs that take 2 clocks).

Interesting. Division is rcp and mul, which should take 5 cycles, but there's also a 9 cycle version. Is this for properly handling division by zero? I don't understand why sin, cos and exp take 2 x 4 cycles, unless they use polynomials of degree four for these which they compute in two iterations?

The ATI SF units are also very interesting:

Technique for approximating functions based on lagrange polynomials

Method and system for approximating sine and cosine functions

Thanks for the references!

When you're done, I'd be interested in your analysis of the lookup table sizes required to produce fast DP results!

I'm currently very busy with a master's thesis, but I'll try to do some quick experiments if I find a minute of extra time...

Anyway, I think it's really a balance between table size, pipeline length, and the number of iterations you're willing to spend. The ARITH17 slides show an overview of the area spent on the lookup tables and the arithmetic logic, for single-precision.

 

[Jawed]

I have the ARITH17 slides (in PDF format), if that's what you mean. Anyway, I think I know where my confusion came from: they use a Booth encoded multiplier.

There's a paper, too, which contains more detail on how the lookup tables are formulated.

Oh, I think I get it. One SFU can compute interpolants for a whole quad at once (there are only small gradients within a quad), while when used for special functions it can only compute one at a time.

Exactly.

I previously thought the 128 stream processors had one MAD unit and one (whole) SFU each. But it's really 8 MAD units sharing 2 SFU's, right? So it takes 4 clock cycles to execute a special function for all eight stream processors.

Yeah. Which is why I like to point out the scheduling hazards associated with instructions that are issued to SF/MI, and why the theoretical MUL here has little value.

This puzzles me about the 518 GFLOPS for G80 at 1.35 GHz that floats around in some places. Is this simply incorrect?

I assume so. If you take the 4 interpolation lanes and call them 1 MUL each, you could argue for it (but the precision isn't there, I presume). I dunno.

Also, doesn't this make the possibility of performing a MUL on the SFU's nearly insignificant? You'd need a shader with lots of muls and little special functions and interpolants. And even then you can 'only' gain 12.5% in GFLOPS.

I can't find it, but Arun or Rys reported that they could access this MUL. But only with a particular driver and only at low performance with a relatively short shader, I think (15% gain). It really seems best to ignore it.

Since each SF can also interpolate the 4 pixels in a quad, it turns out that for every 8 MAD you get 8 interpolated-attributes.

Yeah.

Interesting. Division is rcp and mul, which should take 5 cycles, but there's also a 9 cycle version. Is this for properly handling division by zero?

I'm afraid I didn't really pay attention, I simply noted that there are varying throughputs. Appendix A goes into some detail, including ranges, precision etc.

I don't understand why sin, cos and exp take 2 x 4 cycles, unless they use polynomials of degree four for these which they compute in two iterations?

Perhaps they require biasing first? I'm afraid you'll need someone more mathematical than me to discuss this stuff with.

Jawed

 

[Nick]

I'm afraid I didn't really pay attention, I simply noted that there are varying throughputs. Appendix A goes into some detail, including ranges, precision etc.

Thanks again for the pointer! It confirms my suspicion about the 5 and 9 cycle division. Frankly I believe they should deal with this at the hardware level by using some float bit patterns as 'reciproque of zero'. NaN's allow all non-zero mantissa's, so one can be reserved for this. Only when written to memory it has to be converted to infinity.

No details on log and exp in that appendix though.

 

[Nick]

There's a paper, too, which contains more detail on how the lookup tables are formulated.

Thanks for sending me the paper! I've only read part of it but it doesn't look like it contains any surprises. Their approach for rounding the polynomial's coefficients is interesting though. For my exp and log implementations on the CPU I used Maple to get the minimax coefficients, and then used a brute-force approach to try all the coefficients that are a few ulps higher and lower.